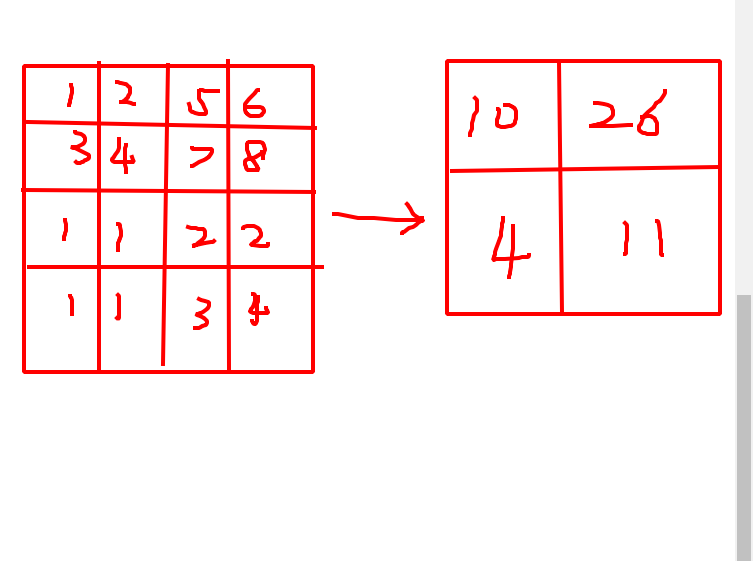
You could do something like this
a = torch.tensor([[[[1.,2,5,6], [3,4,7,8], [1,1,2,2], [1,1,3,4]]]], requires_grad=True)
B, C, H, W = a.shape
kernel = 2
out_h = H // kernel
out_w = W // kernel
rows = torch.arange(0, H, kernel).repeat(out_h)
cols = torch.arange(0, W, kernel).repeat_interleave(out_w)
x0y0 = a[..., cols+0, rows+0]
x0y1 = a[..., cols+0, rows+1]
x1y0 = a[..., cols+1, rows+0]
x1y1 = a[..., cols+1, rows+1]
out = (x0y0 + x0y1 + x1y0 + x1y1).reshape(B, C, out_h, out_w)
print(out)
If you want a different kernel size, then you need to add the necessary xMyN=a[..., cols+M, rows+N] and add them all up.
But this workaround is very prone to errors. I would rather use any of the other solutions given, as they are more robust and will not break that easily.