Hi all,
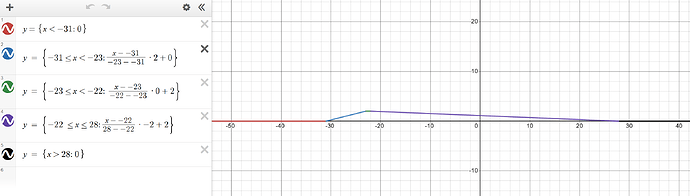
I need to write a custom activation function which should support backward derivative operation.
The behavior of the activation function should vary based on the recieved parameters a and b.
Below, I share my sample code using NumPy to explain my requirement better.
x = torch.linspace(-35,30,4000)
x_numpy=x.data.numpy()
def activation_function(inp,a,b):
'''boundaries -31,28'''
#finding the equation of two points (-31,0),(a,2)
points = [(-31,0),(a,2)]
x_coords, y_coords = zip(*points)
A = vstack([x_coords,ones(len(x_coords))]).T
m_1, c_1 = lstsq(A, y_coords)[0]
#finding the equation of two points [(b,2),(28,0)]
points = [(b,2),(28,0)]
x_coords, y_coords = zip(*points)
A = vstack([x_coords,ones(len(x_coords))]).T
m_2, c_2 = lstsq(A, y_coords)[0]
temp = np.array([])
for i in inp:
if i<-31:
temp = np.concatenate( (temp, [0] ) )
elif i>=-31 and i<a:
#temp = np.concatenate( (temp, [i+31] ) ) #for a=-29
temp = np.concatenate( (temp, [m_1*i+c_1] ) )
elif i>=a and i<=b:
temp = np.concatenate( (temp, [2] ) )
elif i>b and i<28:
#temp = np.concatenate( (temp, [-0.03571*i+1] ) ) #for b=-28
temp = np.concatenate( (temp, [m_2*i+c_2] ) )
else:
temp = np.concatenate( (temp, [0] ) )
return temp
x_numpy_new_1 = activation_function(x_numpy,-29,-28)
plt.figure(figsize=[24,4])
plt.plot(x_numpy,x_numpy_new_1,c='r',label="my_custom_activation_function")
plt.ylim([-0.5,2.5])
plt.xticks(np.arange(min(x_numpy), max(x_numpy)+1, 1.0))
plt.legend(loc='best')
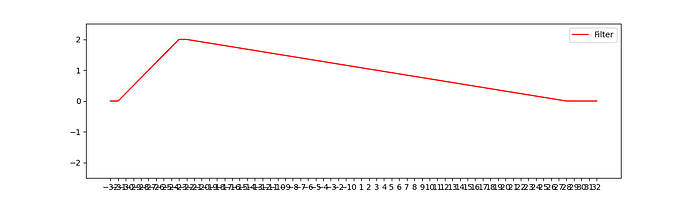
the result should look like this:
As you can see, the function takes a value of 0 below -31 and above 28. -31 and 28 are fixed numbers no matter what. In this example parameter ‘a’ was -29 and parameter ‘b’ was -28. And the function takes a value of 2 between ‘a’ and ‘b’. And between -31,‘a’ and ‘b’,28, I need to calculate the equations first to determine the output values.
Here is the output for other iteration where the function outputs a value of 2 between parameters -23, -22
x_numpy_new_2 = activation_function(x_numpy,-23,-22)
plt.figure(figsize=[24,4])
plt.plot(x_numpy,x_numpy_new_2,c='r',label="my_custom_activation_function")
plt.ylim([-0.5,2.5])
plt.xticks(np.arange(min(x_numpy), max(x_numpy)+1, 1.0))
plt.legend(loc='best')
Final example where the function outputs 2 between parameters -17, -16
x_numpy_new_3 = activation_function(x_numpy,-17,-16)
plt.figure(figsize=[24,4])
plt.plot(x_numpy,x_numpy_new_3,c='r',label="my_custom_activation_function")
plt.ylim([-0.5,2.5])
plt.xticks(np.arange(min(x_numpy), max(x_numpy)+1, 1.0))
plt.legend(loc='best')
Any support will be highly appreciated.
Best wishes…