Hi,
In theory, fully connected layers can be implemented using 1x1 convolution layers. Following are identical networks with identical weights. One implemented using fully connected layers and the other implemented the fully connected network using 1x1 convolutions.
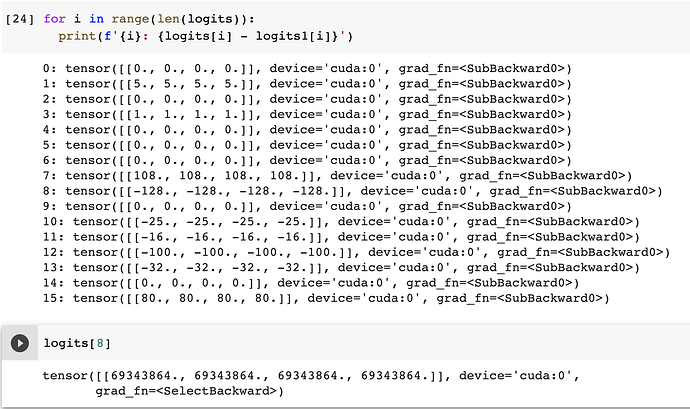
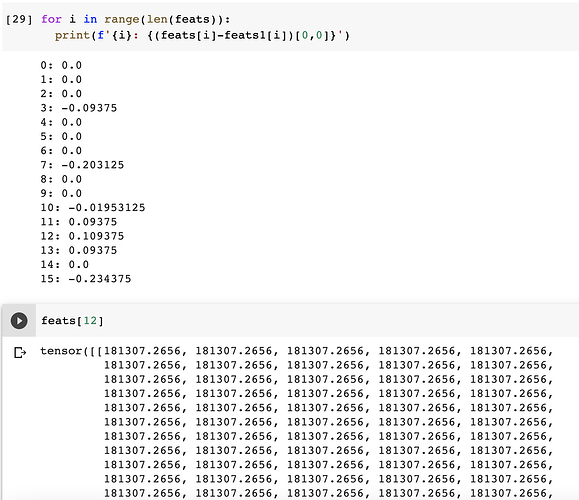
However, the results are different. I am not able to explain the difference in the results. What have I done wrong in the following code?
import torch
import torch.nn
import torch.nn.functional as F
class Model(torch.nn.Module):
def __init__(self, input_dim: int):
super(Model, self).__init__()
self._backbone = torch.nn.Sequential(
torch.nn.Linear(input_dim, 64, bias=True),
torch.nn.ELU(),
torch.nn.Linear(64, 128, bias=True),
torch.nn.ELU(),
torch.nn.Linear(128, 256, bias=True),
torch.nn.ELU(),
)
self._logits = torch.nn.Linear(256, 4, bias=True)
def forward(self, x: torch.Tensor):
feats = self._backbone(x)
logits = self._logits(feats)
return logits, feats
class ModelConv(torch.nn.Module):
def __init__(self, input_dim: int):
super(ModelConv, self).__init__()
self._backbone = torch.nn.Sequential(
torch.nn.Conv2d(input_dim, 64, 1, bias=True),
torch.nn.ELU(),
torch.nn.Conv2d(64, 128, 1, bias=True),
torch.nn.ELU(),
torch.nn.Conv2d(128, 256, 1, bias=True),
torch.nn.ELU(),
)
self._logits = torch.nn.Conv2d(256, 4, 1, bias=True)
def forward(self, x: torch.Tensor):
x = x.unsqueeze(3).permute(0, 2, 1, 3)
feats = self._backbone(x)
logits = self._logits(feats)
feats = feats.squeeze(3).permute(0, 2, 1)
logits = logits.squeeze(3).permute(0, 2, 1)
return logits, feats
if __name__ == '__main__':
input_dim = 256
num_classes = 4
samples = 5
batch_size = 16
torch.manual_seed(2010)
x = torch.randn(batch_size, samples, input_dim)
layers_width = [50, 100, 150]
def init(m):
if hasattr(m, 'weight'):
torch.nn.init.constant_(m.weight, 1)
if hasattr(m, 'bias'):
torch.nn.init.constant_(m.bias, 1)
device = torch.device('cuda:0')
x = x.to(device)
model = Model(input_dim)
model.apply(init)
model.cuda(device)
for p in model.parameters():
assert p.max() == p.min()
logits, feats = model.forward(x)
model1 = ModelConv(input_dim)
model1.apply(init)
model1.cuda(device)
for p in model1.parameters():
assert p.max() == p.min()
logits1, feats1 = model1.forward(x)
print(torch.mean(logits1-logits))
print((feats1-feats).sum())