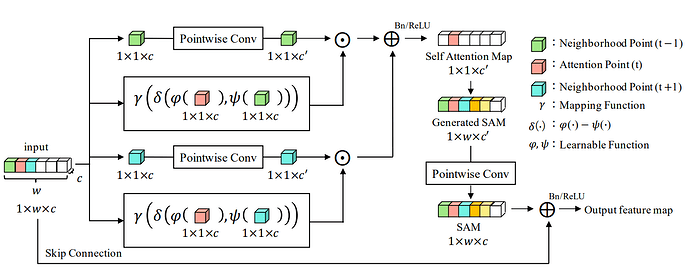
I’m trying to implement the 1D self-attention illustrated in this paper
Specifically, I’m focusing on the following picture:
Below you can find my attempt:
import torch.nn as nn
import torch
#INPUT shape ((B), n_channels, height, width)
class Self_Attention1D(nn.Module):
def __init__(self, in_channels=1, out_channels=3):
super().__init__()
self.pointwise_conv1 = nn.Conv1d(in_channels=in_channels,
out_channels=out_channels, kernel_size=(1,1))
self.pointwise_conv2 = nn.Conv1d(in_channels=out_channels,
out_channels=in_channels, kernel_size=(1,1))
self.phi = MLP(in_size = out_channels, out_size=32)
self.psi = MLP(in_size = out_channels, out_size=32)
self.gamma = MLP(in_size=32, out_size=out_channels)
def forward(self, x):
x = self.pointwise_conv1(x)
phi = self.phi(x.transpose(1,3))
psi = self.psi(x.transpose(1,3))
delta = phi-psi
gamma = self.gamma(delta).transpose(3,1)
out = self.pointwise_conv2(torch.mul(gamma,x))
return out
class MLP(nn.Module):
def __init__(self, in_size, out_size):
super().__init__()
self.in_size = in_size
self.out_size = out_size
self.layers = nn.Sequential(
nn.Linear(in_size, 64),
nn.ReLU(),
nn.Linear(64,128),
nn.ReLU(),
nn.Linear(128,64),
nn.ReLU(),
nn.Linear(64,out_size))
def forward(self, x):
out = self.layers(x)
return out
What it’s not clear to me is, how can we implement the boxed operation in such a way that the delta function takes each single entry and its neighbour one at a time as it is supposed to be by looking at the picture.
I think that my implementation is definitely ignoring locality of the operation.