I would like to implement an initialization identical to tf.truncated_normal_initializer.
I read a suggestion of doing: m.weight.data.normal_(1.0, 0.02).clamp_(min=0,max=2), but it is not good as values with more than two standard deviations from the mean should be discarded and re-drawn, and not clamped to a constant max/min value.
Do you have a suggestion of how can I implement it?
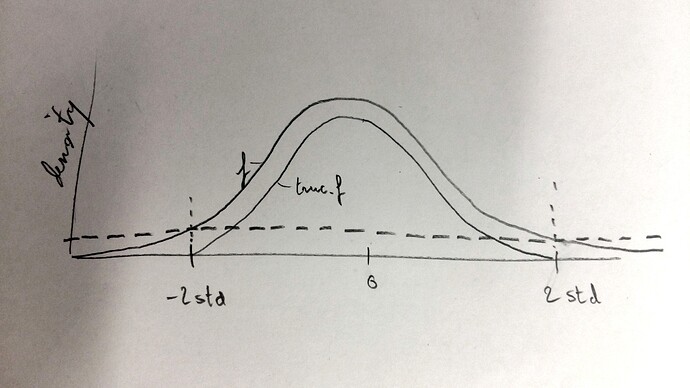
I would suggest a monte-carlo sampling imitating the one used by torch.normal, but instead of using the normal pdf (let’s cal it “f”), you use this pdf:
trunc_f = max( 0 , f - f(2*std) )
In fact, you have to first truncate a centered normal with std=1, do the sampling, then you multiply the values by std and add the mean.
@SivanK - the reason @alexis-jacq suggests you substract 2stdev (or however much you want to truncate) from your normal is because if you do a naive min/max, you’ll end up with two spikes on either end of your curve instead of a nice taper.
Wow, in fact, there are no monte-carlo method behind torch.normal (wich is a backend of the TH normal function from THRandom.c). It is based on the box-muller transform.
The box-muller trick is to sample, uniformly between 0 and 1 two random variables, U1 and U2. Then, you can verify that
Z = sqrt(-2*log(U1)) * cos(2*pi*U2) = R*cos(Theta)
follows a normal distribution. Now, we want to create Z only living between -2 and 2. For this truncation, we still accept all the angles Theta, but we just want the ray R bigger than -2 and smaller than 2. In other words:
-2 <= sqrt(-2*log(U1)) <= 2
iif U1 is uniformly sampled between exp(-2) and 1 
Then you have the python function:
# sample u1:
size = m.weight.size()
u1 = torch.rand(size)*(1-np.exp(-2)) + np.exp(-2)
# sample u2:
u2 = torch.rand(size)
# sample the truncated gaussian ~TN(0,1,[-2,2]):
z = torch.sqrt(-2*log(u1)) * torch.cos(2*np.pi*u2)
m.weight.data = z
This led to a pull request for THRandom.c: https://github.com/torch/TH/pull/4
@uapatira - that’s why I asked this question in the first place 
@alexis-jacq - Thanks for the great answer!
@alexis-jacq This approximation is not close to the true distribution.
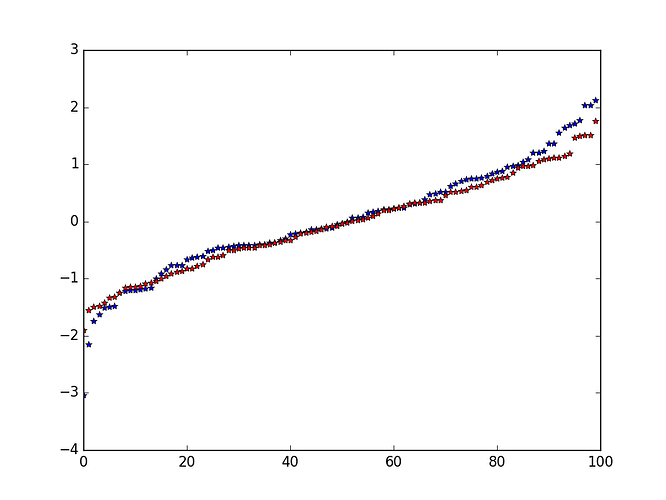
Well it seems ok with plots:
in blue, the normal distribution (sorted)
in red, the truncated distribution (also sorted)
Well, the method confines the random variables to a circle when you want a square [Edit: The square would not work either as it has the wrong marginals, too. One needs the full “other dimension” for each coordinate]. It probably works just fine for the initialisation heuristic, but it is far from general purpose.
(Interestingly, a similar transformation to polar coordinates is the easiest way I know to compute the normalisation constant in the normal transform. If you could apply it to squares you would get a closed form for the normal CDF.)
Best regards
Thomas
I don’t understand why do you want a square… Don’t we want to confine into a circle of ray 2? And anyway, here my example is in 1d, so the circle and the square are the same, it’s the segment [-2, 2]. The box-muller method for truncated normal is already known and used, since this paper: http://oa.upm.es/22659/1/INVE_MEM_2012_153251.pdf
@alexis-jacq I haven’t looked at the paper. But from my simulation, the sampled points are not following the true truncated normal distribution,
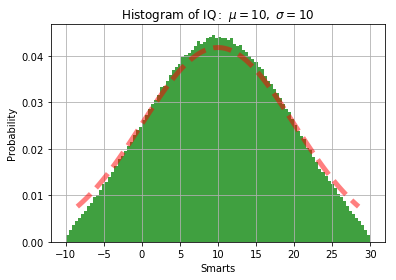
The red line is the pdf given by scipy.stats.truncnorm
This seems to be the picture I had in mind when I said that it was with cutting off too much by restricting to the circle…
If you can do with an approximation, torch.fmod(torch.randn(size),2) might be easiest.
It moves more of the cut-off mass to the center than to the boundaries, but at least the good samples stay where they belong…

Wow, and your approximation takes one line!
So it looks like you take all the element over 2 and put them close to the mean, like in a snake game, and that’s why you have still too many people close to the mean. And it seems that the worst case comes with variance = 1. I would worth to write down the mathematics, to see how far we are from a Gaussian with both methods
Hi Alexis,
Well, I think one of the things is that your sketch seems different from the usual definition of truncated Gaussian.
So what the .fmod in sampling does in terms of pdf is to sum the pdf over all x+sign(x)*cutoff*i | i=0,1,2,… . If the shape of pdf in [cutoff*i, cutoff*(i+1)] were proportional to [0,cutoff], this would be exact. As it is falls of much more quickly than proportional (a 3 std event conditional on the magnitude being at least 2 std is much less likely than a 1 std event). This is why summation puts too much mass in the center. With a smaller cutoff, the pdf in [-cutoff,cutoff] becomes flatter (closer to uniform) and thus the error is more pronounced. And this would further increase if you cut of at less than 1 std, but at some point you might just use a uniform distribution anyway. Even at 1 you could use a cutoff of 2/3 (or so) and then multiply the sample by 3/2 to approximate the truncated normal better (i.e. torch.fmod(torch.randn(size),2/3)*3/2).
In the plain Box-Muller method, you are essentially using two transforms: first that for U_1 uniform on [0,1] R = -sqrt(2 ln(U_1)) has the distribution of the radii in a 2d standard normal, χ(2). Thus that X,Y = sin/cos(U_2) * R will be 2d standard normal. Then you are using that the marginals of the 2d standard normal are 1d standard normals.
If you now restrict R to R <= c, and take the pdf of X close to c, you have only very little of the total mass along the vertical (Y-coordinate) lies in the disc R<=c. This is why the “restricted BM” distribution has the density going to 0 as X approaches c.
But then I would be surprised if the initialisation heuristic broke down on with a simple approximation.
Best regards
Thomas
Ok thanks, now I understand better. So, close to x= 0, all samples should be accepted, since cos(U_2) is small, but with my approach, I still multiply by a restricted R and I make it even smaller. That explains the plot of @ruotianluo where I pass over expected density close to the mean.
It was too beautiful to work…
Once again, I should be more careful when emotions mix with mathematics…
Coming back to this thread after one year.
One simple approximated implementation for truncated_normal to 2*std.
def truncated_normal_(tensor, mean=0, std=1):
size = tensor.shape
tmp = tensor.new_empty(size + (4,)).normal_()
valid = (tmp < 2) & (tmp > -2)
ind = valid.max(-1, keepdim=True)[1]
tensor.data.copy_(tmp.gather(-1, ind).squeeze(-1))
tensor.data.mul_(std).add_(mean)
Hi! Does it implement same thing as https://www.tensorflow.org/api_docs/python/tf/truncated_normal ?
Here is a simpler way to sample values from truncated normal distribution.
from scipy.stats import truncnorm
import torch
def truncated_normal(size, threshold=1):
values = truncnorm.rvs(-threshold, threshold, size=size)
return values
# usage example
x= truncnorm([10, 20], threshold=1) # sample 10x20 sized tensor
x = torch.from_numpy(x).cuda()
Thanks @ruotianluo.
I confirmed that your function is equivalent to scipy truncnorm.
if anyone wants reproduce:
import torch
from scipy.stats import truncnorm
import matplotlib.pyplot as plt
def truncated_normal_(tensor, mean=0, std=1):
size = tensor.shape
tmp = tensor.new_empty(size + (4,)).normal_()
valid = (tmp < 2) & (tmp > -2)
ind = valid.max(-1, keepdim=True)[1]
tensor.data.copy_(tmp.gather(-1, ind).squeeze(-1))
tensor.data.mul_(std).add_(mean)
return tensor
fig, ax = plt.subplots(1, 1)
def test_truncnorm():
a, b = -2, 2
size = 1000000
r = truncnorm.rvs(a, b, size=size)
ax.hist(r, density=True, histtype='stepfilled', alpha=0.2, bins=50)
tensor = torch.zeros(size)
utils.truncated_normal_(tensor)
r = tensor.numpy()
ax.hist(r, density=True, histtype='stepfilled', alpha=0.2, bins=50)
ax.legend(loc='best', frameon=False)
plt.show()
if __name__ == '__main__':
test_truncnorm()
The Tensorflow implementation of truncated_normal can be found on GitHub and references https://people.sc.fsu.edu/~jburkardt/presentations/truncated_normal.pdf (see page 24) there.
Analogous Numpy/PyTorch code would look like
import numpy as np
import torch
def parameterized_truncated_normal(uniform, mu, sigma, a, b):
normal = torch.distributions.normal.Normal(0, 1)
alpha = (a - mu) / sigma
beta = (b - mu) / sigma
alpha_normal_cdf = normal.cdf(alpha)
p = alpha_normal_cdf + (normal.cdf(beta) - alpha_normal_cdf) * uniform
p = p.numpy()
one = np.array(1, dtype=p.dtype)
epsilon = np.array(np.finfo(p.dtype).eps, dtype=p.dtype)
v = np.clip(2 * p - 1, -one + epsilon, one - epsilon)
x = mu + sigma * np.sqrt(2) * torch.erfinv(torch.from_numpy(v))
x = torch.clamp(x, a, b)
return x
def truncated_normal(uniform):
return parameterized_truncated_normal(uniform, mu=0.0, sigma=1.0, a=-2, b=2)
def sample_truncated_normal(shape=()):
return truncted_normal(torch.from_numpy(np.random.uniform(0, 1, shape)))
However in the case of mu=0.0, sigma=1.0, a=-2, b=2, I suspect repeated normal sampling is also fine: 5% of entries need to be resampled each iteration. E.g. since 0.05**5 * 1000000 < 1 one would need roughly 5 iterations for 1M entries.