@alexis-jacq I haven’t looked at the paper. But from my simulation, the sampled points are not following the true truncated normal distribution,
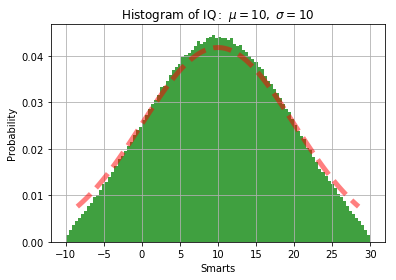
The red line is the pdf given by scipy.stats.truncnorm
2 Likes