Inference Differs with CPU type

1

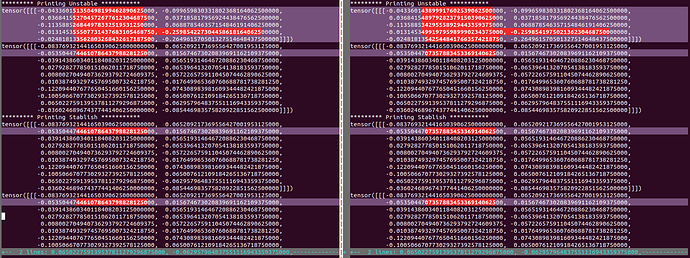
Has any anyone observed differences in CPU calculations on different processors with Torch 1.4.0? Is there a way to fix this? I ran the same code in the same environment (a docker container) on two different machines and got slightly different results on each. The image below shows the differences.

Machine one has Intel(R) Core™ i7-7800X CPU @ 3.50GHz
Machine two has Intel(R) Xeon(R) CPU E5-2670 0 @ 2.60GHz

image
image1746×654 131 KB

With recursive calculations these differences become large enough to change the predictions from my model.

The code below produces the results shown.

#!/usr/bin/env python

import torch
import torch.nn as nn
import torch.nn.functional as F

torch.manual_seed(1)
### No affect
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.enabled = False

torch.set_printoptions(precision=30)

class TestNet(nn.Module):

  def __init__(self, input_dim, hidden_size, depth, observation_dim, dropout=0):
    super(TestNet, self).__init__()
    self.hidden_size = hidden_size
    if depth >= 2:
      self.gru = nn.GRU(input_dim, hidden_size, depth, dropout=dropout)
    else:
      self.gru = nn.GRU(input_dim, hidden_size, depth)
    self.linear_mean1 = nn.Linear(hidden_size, hidden_size)
    self.linear_mean2 = nn.Linear(hidden_size, observation_dim)

  def forward(self, input_seq, hidden=None):
    output_seq, hidden = self.gru(input_seq, hidden)
    if good:
      mean = output_seq
    else:
      mean = self.linear_mean2(F.relu(self.linear_mean1(output_seq))) # BAD
    return mean, hidden

input_dim = 20
hidden_dim = 20
proj_dim = 10

hidden = torch.zeros(1,1,hidden_dim)
hidden_in = torch.zeros(1,1,hidden_dim)
in_tensor = torch.zeros(input_dim)

rnn_thing = TestNet(input_dim, hidden_dim, 1, proj_dim, 0)
rnn_thing.eval()

out, hidden = rnn_thing(in_tensor.view(1,1,-1), hidden=hidden_in, good=False)
print('********* Printing Unstable ***********')
print(out.data)
print(hidden.data)

print('********* Printing Stablish ***********')
out, hidden = rnn_thing(in_tensor.view(1,1,-1), hidden=hidden_in, good=True)
print(out.data)
print(hidden.data)
2

The printed differences seem to be in the range 1e-6, which is most likely due to the limited floating point precision.

Could you explain the issue regarding the changed predictions a bit more?
I.e. how large is the absolute difference after which layer and how many training iterations?
Since these small errors might add up, I wouldn’t expect to get exactly the same outputs after some epochs of training.
However, neither would I expect that one of the machines always produces as “good” model, while the other one fails.

4

Thank you for your response. I should state the problem more clearly. I’m using the same trained model for inference on two different machines and seeing results differ like this. I simplified the problem down to an unintialized network to see where the error was coming from.

To predict, this network is called multiple times parts of a time series and the likelihood for labels is continuously updated. So this slight difference here eventually diverges enough on until the prediction differ.

Since this seems to be a computation issue do you have any advice for keeping things more stable? I’ve tried change the data precision and manually rounding variables. I’m also thinking about ways to make my prediction step less accumulative? Do you have any experience predicting long time series and keeping the predictions real time (eg. outputting results frequently while keeping the RNN state)?

5

You could try to use float64 for all calculations and check the stability again. This would make the execution of your model slower, but could be informative for debugging further.

How often do you need to accumulate the predictions and how many values do you have?
Could you post an example of such a prediction, which is changed due to the floating point errors?

6

Thanks, but unfortunately, it appears GRU only works with float32. I’ll keep trying.

The predictions come from google’s UISRNN UISRNN repository where they accumulate loss it also accumulates computation differences. How often? Beamwidth times (10 is default) for every step in the input sequence so I’d say a lot?