When is it best to use normalization:
# consist positive numbers
normalized_data = (data / data.max()) * 2 - 1
instead of standardization:
nomalized_data = (data - data.mean()) / sqrt(data.var())
1 Like
What we see in here:
An alternative approach to Z-score normalization (or standardization) is the so-called Min-Max scaling (often also simply called “normalization” - a common cause for ambiguities).
In this approach, the data is scaled to a fixed range - usually 0 to 1.
The cost of having this bounded range - in contrast to standardization - is that we will end up with smaller standard deviations, which can suppress the effect of outliers.
Can someone explain the selected part?
I think the code you have mentioned doesn’t correspond to min-max.
Z-score is fine. However, min_max_norm = (data - data.min())/(data.max() - data.min())
For normalisation, the values are squashed in [0, 1]. If you have an outlier say data.max() the transformed values will be very small for min_max_norm(max in denominator) for the majority of samples. Thereby affecting the statistics of your transformed distribution.
This is a classic fight. But you have to look at the pre and post data to get an idea
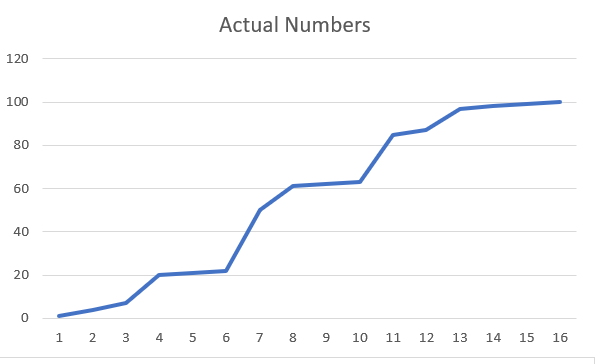
The normalization and standardization affects this array in the following manner
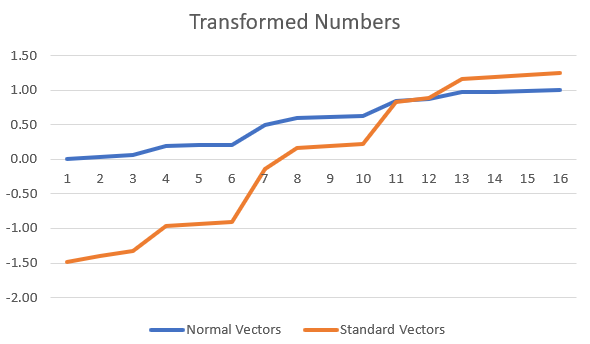
We can see the Standard Array represents the original array better.
Inference
-
If you have clusters of data points in your dataset, it is better to use Standard Scaling. Normal Scaling will not create a lot of variance between the points to close to each other, as can be seen in the images
-
If you have anomalies in your data, it is better to use Standard Scaling as Normal Scaling will skew the data
1 Like
Normal Scaling will not create a lot of variance between the points to close to each other, as can be seen in the images
Can you explain this moment in more details if that possible pls?
I think the code you have mentioned doesn’t correspond to min-max.
If normalization squashes data into [-1; -1] then is my norm code version possible to exist?
The range will be [-1, 1], however, it is not referred to min-max normalisation. To keep the range [-1, 1], typically min-max normalisation is employed.
But which parameter(property) will be differ in such cases: my version of squashing into [-1;1] and min-max normalization into the same range?
You can compare the mean of the scaled values. I am computing the mean as it’s easy to compute.
u_your = (2*u_old - x_max)/(x_max)
whereas, u_minmax = (u_old - x_min)/(x_max - x_min)
you can see that the new means are going to be different after applying the scaling. Correspondingly you can also compute the variance to check if they differ.
Maybe you can additionally explain the first statement
In standarization, technically, there is no limit as to what value can the extremes of output have. In case of normalization, however, the most extreme values will be equal to 1 and -1.
This will suppress the effect of outliers. Why?
For example lets consider a situation when in dataset feature A has a very large variance and feature B has very small (i.e. we expect to find a value of A far from mean quite often, but finding a value of B far from mean is something very unusual). This is a vital information, as finding an example with a very extreme value of B might suggest that this example is an anomaly/ positive/ negative or whatever you want to detect, and finding an extreme value of A is not a very outstanding thing.
After standarization, the extreme values of B will be much further from the zero than values of A, whereas after normalization, in both cases the most extreme values will be equal to 1 and -1. Therefore, the information that an extreme value of B is much more important than an extreme value of A is lost, because in the end, values of these extremes will be equal.
Thanks.
You’ve given a good example.