Is there any research about value distribution of Conv's weight

1

I find that most CONV’s weights are distributed in a small range, a subset of [-1,1].
So I did some works based on this, and I want to know if there was any research paper or explanation about this

2

I couldn’t find the original paper which proposes the importance of weight normalization.
However, the reason is simple. The network can be converged with the values in range of [-1, 1]

Here’s a sequence of multiplication of 3 numbers

  1. 10 x 10 x 10
  2. 0.1 x 0.1 x 0.1

Convergence/divergence is important. We can easily handle the value of 0 but not 1000000000000…

1 Like
3

Thank you, your words inspired me.
I searched weight normalization and I don’t know is that what you said.
Seems like Weight Normalization is helpful to training, and was introduced in this paper.
Is there any evidence that torch implemented this?
And looks like weight normalization is an optional operation in models.
Is there any evidence showing that a network’s weight will be normalized

4

@Forceless

As far as i could find, in the torch documentation for conv2d, the weights of conv2d
https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html#torch.nn.Conv2d

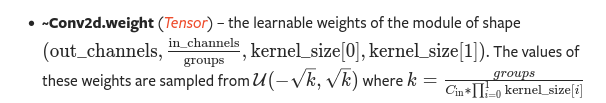
image

import math
import torch
from torch.autograd import grad
import torch.nn as nn

m = nn.Conv2d(16, 33, 3, stride=2)
input = torch.randn(20, 16, 50, 100)
output = m(input)

# According to the equation
k = math.sqrt(1.0/(16 * 3 *3))
print([-k, k])

# UNIT TEST
print([torch.min(m.weight), torch.max(m.weight)])

[-0.08333333333333333, 0.08333333333333333]
[tensor(-0.0833, grad_fn=<MinBackward1>), tensor(0.0833, grad_fn=<MaxBackward1>)]
1 Like
5

I have a question.
It looks like the weight was just initialized like that.
After several epochs of training, did weight value still distributed in this range

6

Nope, the weights are just trained to minimize the loss.
If there is no constraint like clip or something, the weights can be varied in free.

2 Likes
7

Yes, that’s what I mean.