Hello I’m trying to implement some recursive tensor operation like below.
But, my implementation’s training speed seems too slow.
I think using for statements or flips make this operation slower.
Is there any way to speed this up? Whether jit or something.
Thank you.
get l
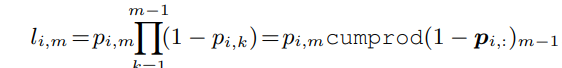
get q
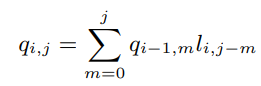
get s
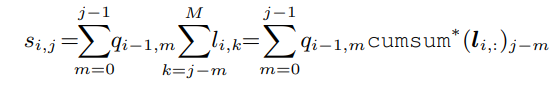
Code
class DifferentiableDurationModeling(nn.Module):
def __init__(self):
super().__init__()
def _get_attn_mask(self, phon_lens, mel_lens):
phon_mask = ~get_mask_from_lengths(phon_lens)
mel_mask = ~get_mask_from_lengths(mel_lens)
return phon_mask.unsqueeze(-1) * mel_mask.unsqueeze(1), phon_mask
def forward(self, p, phon_lens, mel_lens):
attn_mask, phon_mask = self._get_attn_mask(phon_lens, mel_lens)
p = p * attn_mask
l = self._get_l(p, attn_mask)
l = l * attn_mask
dur = self._get_duration(l)
dur = dur * phon_mask
q = self._get_q(l)
q = q * attn_mask
s = self._get_s(q, l)
s = s * attn_mask
return s, l, q, dur
def _get_duration(self, l):
m = torch.arange(1, l.shape[-1] + 1)[None, :].expand_as(l).to(l.device)
return torch.sum(m * l, dim=-1)
def _get_l(self, p, mask):
# getting l is numerically unstable for the gradient computation.
# Paper's Author resolve this issue by computing this product in the log-space
_p = torch.log(mask[:, :, 1:].float() - p[:, :, 1:] + 1e-8)
p = torch.log(p + 1e-8)
com = torch.cumsum(_p, dim=-1)
l_0 = com[:, :, -1].unsqueeze(-1)
l_1 = p[:, :, 1].unsqueeze(-1)
l_m = com[:, :, :-1] + p[:, :, 2:]
l = torch.cat([l_0, l_1, l_m], dim=-1)
l = torch.exp(l)
return l
def _variable_kernel_size_convolution(self, x, y, length):
matrix = torch.flip(x.unsqueeze(1) * y.unsqueeze(-1), dims=[-1])
output = torch.flip( torch.cat([torch.sum(torch.diagonal(matrix, offset=idx, dim1=-2, dim2=-1), dim=1).unsqueeze(1) for idx in range(length)], dim=1), dims=[1] )
return output
def _get_q(self, l):
length = l.shape[-1]
q = [l[:, 0, :]]
if l.shape[-1] > 1:
for i in range(1, l.shape[1]):
q.append(self._variable_kernel_size_convolution(q[i-1], l[:, i], length))
q = torch.cat([_.unsqueeze(1) for _ in q], dim=1)
return q
def _reverse_cumsum(self, x):
return torch.flip(torch.cumsum(torch.flip(x, dims=[-1]), dim=-1), dims=[-1])
def _get_s(self, q, l):
length = l.shape[-1]
l_rev_cumsum = self._reverse_cumsum(l)
s = [l_rev_cumsum[:, 0, :]]
if l.shape[-1] > 1:
for i in range(1, q.shape[1]):
s.append(self._variable_kernel_size_convolution(q[:, i-1], l_rev_cumsum[:, i], length))
s = torch.cat([_.unsqueeze(1) for _ in s], dim=1)
return s