Hi,
I have been working on quantization for a while and while working on a project in which I was planning to perform the more efficient bit-shift rescaling instead of a float multiplication, I have noticed some discrepancies with my mathematical model. After digging deeper in the implementation of my code, PyTorch and FBGEMM, I made some tests to check where the source of the error lies.
For the test I ran the following code:
import torch
import random
import numpy as np
import pandas as pd
from collections import defaultdict
from matplotlib import pyplot as plt
from torch.quantization.observer import MinMaxObserver
SEED = 100
np.random.seed(SEED)
torch.manual_seed(SEED)
random.seed(SEED)
SHAPE_IN = 10
SHAPE_OUT = 10
BS = 100
MIN = -4
MAX = 4
class M(torch.nn.Module):
def __init__(self):
super(M, self).__init__()
# QuantStub converts tensors from floating point to quantized
self.quant = torch.quantization.QuantStub()
self.fc = torch.nn.Linear(SHAPE_IN, SHAPE_OUT, bias=False)
# DeQuantStub converts tensors from quantized to floating point
self.dequant = torch.quantization.DeQuantStub()
def forward(self, inp):
# manually specify where tensors will be converted from floating
# point to quantized in the quantized model
inp = self.quant(inp)
x = self.fc(inp)
# manually specify where tensors will be converted from quantized
# to floating point in the quantized model
x = self.dequant(x)
return x
def main():
# create a model instance
model_fp32 = M()
# model must be set to eval mode for static quantization logic to work
model_fp32.eval()
# attach a global qconfig, which contains information about what kind
# of observers to attach. Use 'fbgemm' for server inference and
# 'qnnpack' for mobile inference. Other quantization configurations such
# as selecting symmetric or assymetric quantization and MinMax or L2Norm
# calibration techniques can be specified here.
model_fp32.qconfig = torch.quantization.QConfig(
activation=MinMaxObserver.with_args(dtype=torch.quint8),
weight=MinMaxObserver.with_args(dtype=torch.qint8)
)
# Prepare the model for static quantization. This inserts observers in
# the model that will observe activation tensors during calibration.
model_fp32_prepared = torch.quantization.prepare(model_fp32)
# calibrate the prepared model to determine quantization parameters for activations
# in a real world setting, the calibration would be done with a representative dataset
input_fp32 = torch.randn((BS, SHAPE_IN))
model_fp32_prepared(input_fp32)
# Convert the observed model to a quantized model. This does several things:
# quantizes the weights, computes and stores the scale and bias value to be
# used with each activation tensor, and replaces key operators with quantized
# implementations.
model_int8 = torch.quantization.convert(model_fp32_prepared)
return model_int8
def test(val, model_int8):
input_fp32 = torch.ones(
(BS, SHAPE_IN)) * val # constant tensor with entries = val
# compute quantized result with pytorch quantization
pytorch_res = model_int8(input_fp32)
return pytorch_res
def make_plot():
d = defaultdict(list)
model_int8 = main()
for val in np.arange(MIN, MAX, 0.01):
pyt_res = test(val, model_int8)
d['val'].append(val)
for i in range(SHAPE_OUT):
d[f'pyt_res_{i}'].append(pyt_res[0][i].item())
figsize = (1, 25)
for i in range(SHAPE_OUT):
plt.figure(figsize=figsize)
df_a = pd.DataFrame(data={k: v for k, v in d.items() if k in ['val', f'pyt_res_{i}']})
df_a.plot(x='val')
plt.savefig(f"./experimental/res_{i}.png")
plt.close()
if __name__ == '__main__':
make_plot()
The operation performed here is basically a single matrix-vector product. Which was even simplified to have the inputs with all the same values. This means that the operation can be seen as:
Y = WX = W [val ,val, val]^T = torch.sum(W, dim= 1) * val
Example:
W = [[ 1, 10],
[15, 7]|
X = [5, 5]^T
Y = WX = [11, 22]^T * 5 = [55, 110]^T
In my example what I am doing is the following, given a NN, I prepare it for quantization using 100 example datapoints. After converting it, I generate datapoints in the range [-4, 4] and probe the NN and check the output of ever feature.
EXPECTED BEHAVIOUR:
Given the math, and the nature of the inputs (single value). The output of the network for each feature should be monotonic. This means it should look like a clamped ramp (either negative or positive depending on the weight).
RESULTS and OBSERVATIONS:
To have an additional control, I checked also how TFLite behaves. My model and TF show for the same test the same behaviour. The output starts from the boundary of the range, when increasing the value of the input the output starts increasing/decreasing linearly until it reaches the other boundary of the range. So far so good.
PyTorch instead does not she the same behaviour. At least, it does not show that for SHAPE_IN > 1. Here are some plots:
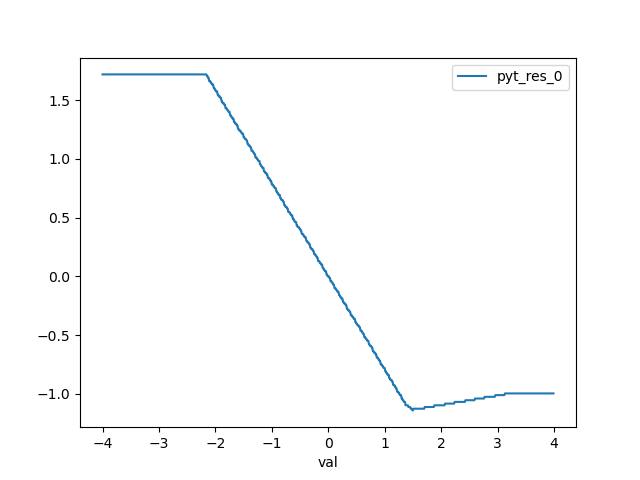
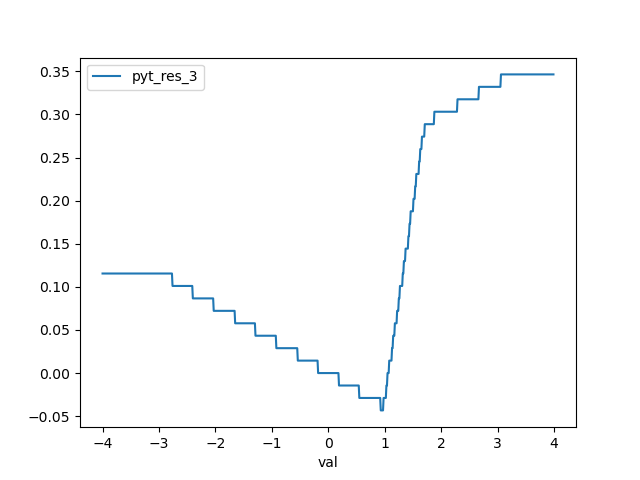
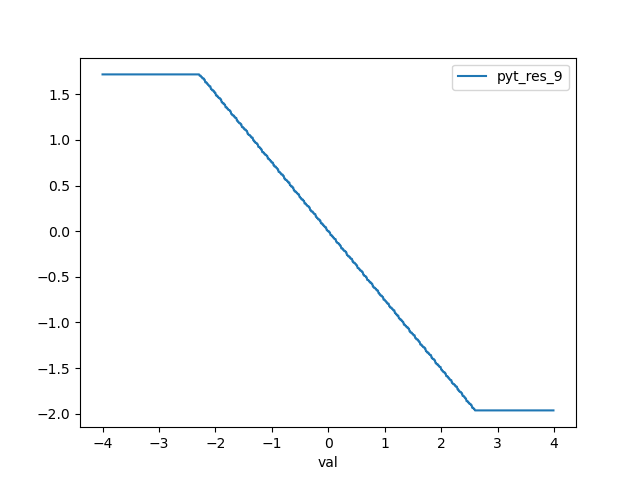
- pyt_res_9 is the 10th output feature and shows the correct trend (the slope could be positive as well)
- pyt_res_0 is the 1st output feature and shows a change of slope at a certain point in the range
- pyt_res_3 is the 4th output feature and shows twice a change of slope in the range
What is going on? Is this a bug or is there some intended behaviour I am not aware about?