Dear all,
I need to imitate a mathematical function (u(x,y)) by a neural network.
The loss I need to minimize is (-u’‘(x,y)-f(x,y))^2 where u’’ is the second derivative of u and f is a function corresponding to this second derivative. In fact, I am comparing the Laplacian of both functions.
In other word, I am trying to first determine u’’ for a given f(x,y), and after, using autograd pytorch function, I try to estimate u.
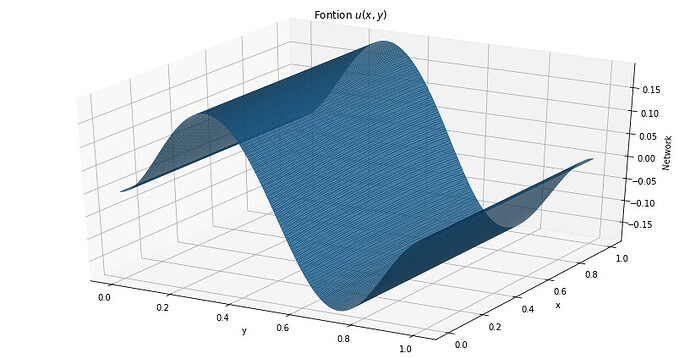
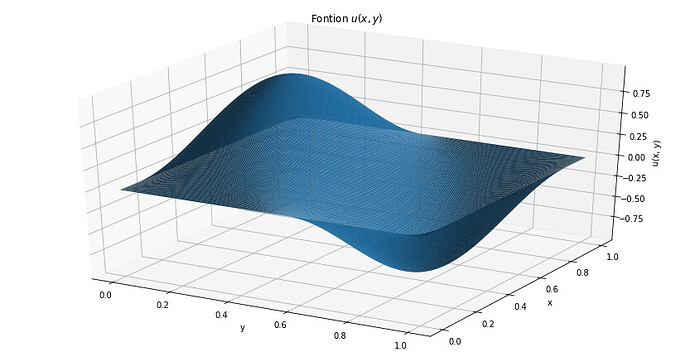
The following code is working fine but the second dimension (y) is not taken into account. See the 2 graphs after the codes : the 1st one stands for the nnfunction and the second one is the real function I wish to imitate.
Any clue why it still does not work properly ?
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
learning_rate = 0.01
num_epochs = 200
N = 200
A = []
U = lambda x: torch.sin(torch.pi * x[0]) * torch.sin(2 * torch.pi * x[1])
f = lambda x, u: (5 * torch.pi**2* torch.sin(torch.pi * x[0]) * torch.sin(2 * torch.pi * x[1]))
x = np.linspace(0, 1, N)
y = np.linspace(0, 1, N)
z = []
for i in range(N):
z.append([x[i],y[i]])
input = torch.tensor(z).to(dtype = torch.float32).requires_grad_(True)
class Net(nn.Module):
def init(self):
super(Net, self).init()
self.fc = nn.Sequential(nn.Linear(2, 64), nn.Tanh(), nn.Linear(64, 1, bias = False))
self.l1 = nn.Linear(2,128,)
self.l2 = nn.Linear(128,10)
self.l3 = nn.Linear(10,1)
def forward(self,input):
x = input[0]
y = input[1]
out = F.tanh(self.l1(input))
out = F.tanh(self.l2(out))
out = self.l3(out)
return out * x * (1-x) * y * (1-y)
model = Net()
gradient = torch.optim.Adam(model.parameters(), lr = learning_rate)
def loss(input, U, A, f):
nablaU = None
for i in input:
output = model(i)
#print(“output”, output)
Uneuronal_dx = torch.autograd.grad(output, i, grad_outputs = torch.ones_like(output), create_graph=True, retain_graph=True)[0]
#print(“Uneuronal_dx”, Uneuronal_dx)
Uneuronal_d2x = torch.autograd.grad(Uneuronal_dx[0], i, create_graph=True, retain_graph=True)[0]
#print(“Uneuronal_d2x”, Uneuronal_d2x)
Uneuronal_dy = torch.autograd.grad(output, i, grad_outputs = torch.ones_like(output), create_graph=True, retain_graph=True)[0]
#print("Uneuronal_dy", Uneuronal_dy)
Uneuronal_d2y = torch.autograd.grad(Uneuronal_dy[1], i, create_graph=True, retain_graph=True)[0]
#print("Uneuronal_d2y", Uneuronal_d2y)
v = torch.unsqueeze(torch.pow(torch.sub(torch.mul(torch.add(Uneuronal_d2x[0], Uneuronal_d2y[1]), -1),f(i, U)), 2), dim=-1)
#print("v", v)
if nablaU is None:
nablaU = v
#print("nablaU", nablaU)
else:
nablaU = torch.cat( (nablaU ,v), dim=0)
#print("nablaU", nablaU)
return(torch.mean(nablaU))
for i in range(num_epochs):
gradient.zero_grad()
l = loss(input, U, A, f)
l.backward()
print(“loss”, l)
gradient.step()
def u_plot(x, y):
return np.sin(np.pi * x) * np.sin(2 * np.pi * y)
input1 = input[:,0].detach().numpy()
input2 = input[:,1].detach().numpy()
output = []
for i in input:
output.append([model.forward(i).detach().numpy()])
output = np.array(output).reshape(N, 1)
fig = plt.figure()
plt.subplots(figsize=(15, 8))
ax = plt.axes(projection=‘3d’)
X, Y = np.meshgrid(input1, input2)
ax.plot_surface(Y, X, output, rstride=1, cstride=1, edgecolor=‘none’)
ax.set_title(‘Fontion $u(x,y)$’);
ax.set_xlabel(‘y’)
ax.set_ylabel(‘x’)
ax.set_zlabel(‘Network’)
fig = plt.figure()
plt.subplots(figsize=(15, 8))
ax = plt.axes(projection=‘3d’)
X, Y = np.meshgrid(input1, input2)
ax.plot_surface(Y, X, u_plot(X, Y), rstride=1, cstride=1, edgecolor=‘none’)
ax.set_title(‘Fontion $u(x,y)$’);
ax.set_xlabel(‘y’)
ax.set_ylabel(‘x’)
ax.set_zlabel(‘u(x, y)’);