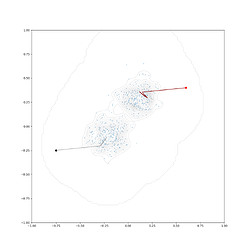
Got something working for vectorized calculation of log probability. I have noticed this can gobble up memory fast if you have large numbers of points. Would welcome any more thoughts. Here is a class to implement it:
import torch
from torch.distributions import MultivariateNormal, Normal
from torch.distributions.distribution import Distribution
class GaussianKDE(Distribution):
def __init__(self, X, bw):
"""
X : tensor (n, d)
`n` points with `d` dimensions to which KDE will be fit
bw : numeric
bandwidth for Gaussian kernel
"""
self.X = X
self.bw = bw
self.dims = X.shape[-1]
self.n = X.shape[0]
self.mvn = MultivariateNormal(loc=torch.zeros(self.dims),
covariance_matrix=torch.eye(self.dims))
def sample(self, num_samples):
idxs = (np.random.uniform(0, 1, num_samples) * self.n).astype(int)
norm = Normal(loc=self.X[idxs], scale=self.bw)
return norm.sample()
def score_samples(self, Y, X=None):
"""Returns the kernel density estimates of each point in `Y`.
Parameters
----------
Y : tensor (m, d)
`m` points with `d` dimensions for which the probability density will
be calculated
X : tensor (n, d), optional
`n` points with `d` dimensions to which KDE will be fit. Provided to
allow batch calculations in `log_prob`. By default, `X` is None and
all points used to initialize KernelDensityEstimator are included.
Returns
-------
log_probs : tensor (m)
log probability densities for each of the queried points in `Y`
"""
if X == None:
X = self.X
log_probs = torch.log(
(self.bw**(-self.dims) *
torch.exp(self.mvn.log_prob(
(X.unsqueeze(1) - Y) / self.bw))).sum(dim=0) / self.n)
return log_probs
def log_prob(self, Y):
"""Returns the total log probability of one or more points, `Y`, using
a Multivariate Normal kernel fit to `X` and scaled using `bw`.
Parameters
----------
Y : tensor (m, d)
`m` points with `d` dimensions for which the probability density will
be calculated
Returns
-------
log_prob : numeric
total log probability density for the queried points, `Y`
"""
X_chunks = self.X.split(1000)
Y_chunks = Y.split(1000)
log_prob = 0
for x in X_chunks:
for y in Y_chunks:
log_prob += self.score_samples(y, x).sum(dim=0)
return log_prob
Here’s a toy example working with gradients:
from sklearn.datasets import make_blobs
from torch.optim import LBFGS
# centers of blobs we'll try to find through optimization
# are at (0.1, 0.3) and (-0.2, -0.1)
X, y = make_blobs(5000, centers=[[0.1,0.3],[-0.2,-0.1]], cluster_std=0.1)
kde = GaussianKDE(X=torch.tensor(X, dtype=torch.float32), bw=0.03)
test_pts = torch.tensor([[-0.75,-0.25],[0.6,0.4]], requires_grad=True)
optimizer = LBFGS([test_pts])
for _ in range(10): # take 10 optimization steps
def closure():
optimizer.zero_grad()
loss = -kde.log_prob(test_pts)
loss.backward()
return loss
optimizer.step(closure)
test_pts
>>> tensor([[-0.2470, -0.1488],
[ 0.1720, 0.3189]], requires_grad=True)