Hey guys, I am trying to recreate results of “The Lottery Ticket Hypothesis” by Frankle et al. They are using CIFAR-10 which has 50K training images. Using a batch size = 64 gives 781 iterations/steps in one epoch.
For VGG-18 & ResNet-18, the authors propose the following learning rate schedule
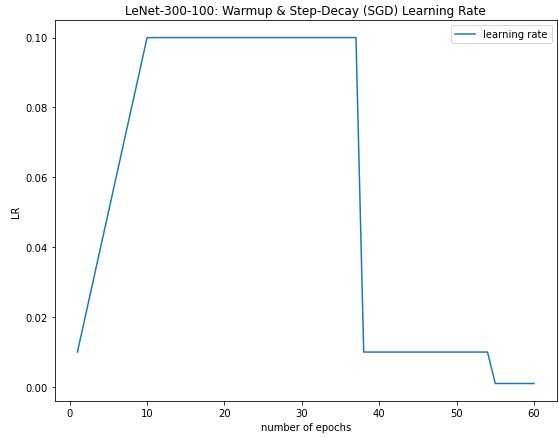
- Linear learning rate warmup for first k = 7813 steps from 0.0 to 0.1
After 10 epochs or 7813 training steps, the learning rate schedule is as follows-
-
For the next 21094 training steps (or, 27 epochs), use a learning rate of 0.1
-
For the next 13282 training steps (or, 17 epochs), use a learning rate of 0.01
-
For any remaining training steps, use a learning rate of 0.001
I have implemented this in TensorFlow2 as follows:
from typing import Callable, List, Optional, Union
class WarmUp(tf.keras.optimizers.schedules.LearningRateSchedule):
"""
Applies a warmup schedule on a given learning rate decay schedule.
Args:
initial_learning_rate (:obj:`float`):
The initial learning rate for the schedule after the warmup (so this will be the learning rate at the end
of the warmup).
decay_schedule_fn (:obj:`Callable`):
The schedule function to apply after the warmup for the rest of training.
warmup_steps (:obj:`int`):
The number of steps for the warmup part of training.
power (:obj:`float`, `optional`, defaults to 1):
The power to use for the polynomial warmup (defaults is a linear warmup).
name (:obj:`str`, `optional`):
Optional name prefix for the returned tensors during the schedule.
"""
def __init__(
self,
initial_learning_rate: float,
decay_schedule_fn: Callable,
warmup_steps: int,
power: float = 1.0,
name: str = None,
):
super().__init__()
self.initial_learning_rate = initial_learning_rate
self.warmup_steps = warmup_steps
self.power = power
self.decay_schedule_fn = decay_schedule_fn
self.name = name
def __call__(self, step):
with tf.name_scope(self.name or "WarmUp") as name:
# Implements polynomial warmup. i.e., if global_step < warmup_steps, the
# learning rate will be `global_step/num_warmup_steps * init_lr`.
global_step_float = tf.cast(step, tf.float32)
warmup_steps_float = tf.cast(self.warmup_steps, tf.float32)
warmup_percent_done = global_step_float / warmup_steps_float
warmup_learning_rate = self.initial_learning_rate * tf.math.pow(warmup_percent_done, self.power)
return tf.cond(
global_step_float < warmup_steps_float,
lambda: warmup_learning_rate,
lambda: self.decay_schedule_fn(step - self.warmup_steps),
name=name,
)
def get_config(self):
return {
"initial_learning_rate": self.initial_learning_rate,
"decay_schedule_fn": self.decay_schedule_fn,
"warmup_steps": self.warmup_steps,
"power": self.power,
"name": self.name,
}
boundaries = [21093, 34376]
values = [0.1, 0.01, 0.001]
learning_rate_fn = tf.keras.optimizers.schedules.PiecewiseConstantDecay(boundaries, values)
warmup_shcedule = WarmUp(initial_learning_rate = 0.1, decay_schedule_fn = learning_rate_fn, warmup_steps = 7813)
optimizer = tf.keras.optimizers.SGD(learning_rate = warmup_shcedule, momentum = 0.9, decay = 0.0, nesterov = False)
I then train model using “tf.GradientTape” and view the learning rate as follows:
optimizer._decayed_lr('float32').numpy()
The resulting learning during the 60 epochs of training can be viewed:
You can access the complete code here. Since I am new to PyTorch, can you show me how I can achieve the same learning rate scheduler in torch?
Thanks