[LINEAR ALGEBRA] [QUESTION] Inverse

#1

Quick question about an implementation choice (didn’t feel appropriate to raise on github)
Psuedo-inverses are proper inverses when a matrix is square + full rank.
It seems like the implementation in torch isn’t doing anything to discover rank and so can’t fall back on classical inverse algorithms for efficiency.

I am playing with this example:

import torch
nrows = 10000
ncols = 10000
torch.inverse(torch.rand(nrows,ncols).cuda())


CPU times: user 3.8 s, sys: 141 ms, total: 3.94 s
Wall time: 927 ms

swapping that last line for torch.pinverse(torch.rand(nrows,ncols).cuda()) yields

CPU times: user 2min 17s, sys: 1.95 s, total: 2min 19s
Wall time: 20.7 s

So, even with added overhead to discover rank with something like Cholesky (for which it seems an implementation exists), large speedups can be gained.

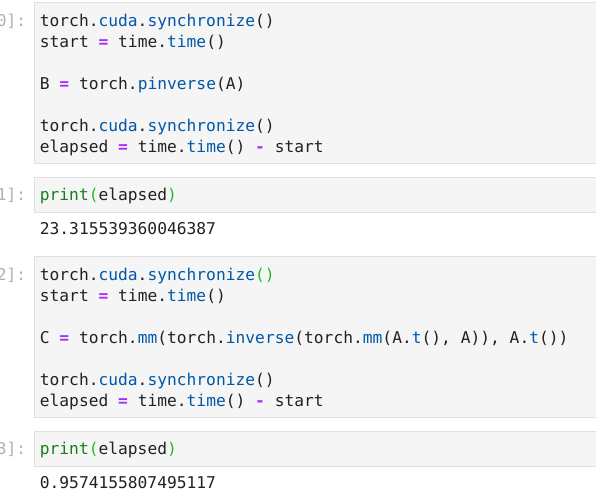
What’s going on under the hood with pseudo-inverse and why is it taking so much longer? mat-mult is sub-second, classical inversion for full-rank operators is sub-second, so even manual-construction wins out:

A = torch.rand(nrows,ncols).cuda()
torch.mm(torch.inverse(torch.mm(A.t(), A)), A.t())

CPU times: user 3.67 s, sys: 167 ms, total: 3.83 s
Wall time: 1.09 s

Moreover, sometimes pinverse runs out of memory, but the latter won’t (a kernel restart allows pinverse to run again), and the solutions do seem to agree on average:

image
image787×430 42.5 KB

#2

Hey,

One thing to be careful of here is that the CUDA api is asynchronous. So without the appropriate torch.cuda.synchronize() calls, you shoud not read too much into these timings.

Still you can see here that we use LU factorization for the inverse and delegate all the heavy lifting to magma.
The pinverse is here on the other hand and uses svd (done by magma as well). Note that it needs to handle batches of inputs.

Quick question about an implementation choice

Definitely open to discussions!

1 Like
#3

thanks so much for the clarification. I’m a maths person who has only used CPUs to date, finally got a GPU to play around with. So, I’m not exactly sure where those calls should go.

The differences in algos though does explain a lot of the difference between my one-liner and the psuedo-inverse method; I really appreciate the linking to the source files, as it’s a large library to sort through!

A cholesky-based inverse may provide some major gains; c.f matlab’s benchmarks in this (admittedly decade old, but still relevant I think) paper: https://arxiv.org/pdf/0804.4809.pdf

#4

correct me if I’m wrong, but as far as I understand, deep-learning networks induce operators that are very ill-conditioned. So, my assumption is that pinverse is a often-called function during training. Is that the case? If not, then I’m not so sure how helpful work on improving it would be.

#5

I wouldn’t say it is a very commonly used operator in general for neural nets. But it is useful and we do want make sure we’re not making obvious mistake here.
That being said, advanced users do have access to all the “low level” functions like lu, svd, getr etc and can use the one they know fits best their use case.

So, even with added overhead to discover rank

Considering that we have both usecases, what would be the overhead here of checking the rank for people that have known non-invertible matrices?

#6

good question. out of curiosity, how does the development team think of overhead? Would numerical tests suffice (perhaps calling .cpu() to collect results at the end of my operations to account for the async?), or are you looking for a Big-O analysis for rank reveal + LU over straight SVD? I’d need to look into the specifics of the magma implementation for that (well, frankly, I have some friends in the department who’d be better suited for that).

#7

perhaps calling .cpu() to collect results at the end of my operations to account for the async?

You can do something like:

torch.cuda.synchronize()
start = time.time()

# your_op

torch.cuda.synchronize()
elapsed = time.time() - start

how does the development team think of overhead?

I am not working on perfs explicitly so the definitive answer will definitely be given by the relevant people on github :wink:
But even though the Big-O notation is a good hint, I think actual runtime will be the most important.
Also such choice can depend on the input size, batch size, etc.

cc @VitalyFedyunin what do you think?

#8

Thanks!
Pretty similar benchmark.
image

Card: RTX2080S, don’t know how this may differ on better hadware. But the stark difference is a clue for an opportunity to improve performance out of the box. I can do some more numerical studies and see if I can get insight to the theoretical cost question

#9

That sounds good.

After a quick offline chat with Vitaly, I think we would be happy to add some heuristics here.
Unfortunately, my linear algebra is a bit rusty but if you could open an issue on github with some details on the heuristic you want to use (and a quick idea why). And a script that can be used to get a first idea of the impact on runtime both for full rank, not full rank matrices and ill conditioned matrices.
I think we can then build on that to make sure that the general penalty in time is small enough for the benefit we get.

1 Like
#10

You can quite update pinverse implementation as it is easy to extract rank from svd calls results here https://github.com/pytorch/pytorch/blob/6debc28964872e26724764e213c40db366327f95/aten/src/ATen/native/LinearAlgebra.cpp#L94

#11

that sounds good. if we can agree on a good benchmarking test, I can devote a little time to experimenting with it.

#12

while I don’t often code in c++, I can totally follow along with that snippet based on the math (also a testament to well-written code).

however, while SVD is rank-revealing, I think what I’d propose is to avoid the cost of computing it altogether potentially, since that seems to be the bottleneck. My demo was just on full-rank operators, and that SVD implementation you linked is more stable for ill-conditioned matrices.