Hi, I’m trying to implement neural architecture search in a way that resembles what’s being done in the “Pay Attention When Required” paper.
In short, what they do is use what they call “stochastic blocks”, which get one input, pass it through N different blocks, and then compute a linear combination of the N outputs to combine them into a single one. They optimize those coefficients just like any parameter, and then visualize them so as to understand which block is “preferrable” for that layer.
A picture probably explains it better than i did:
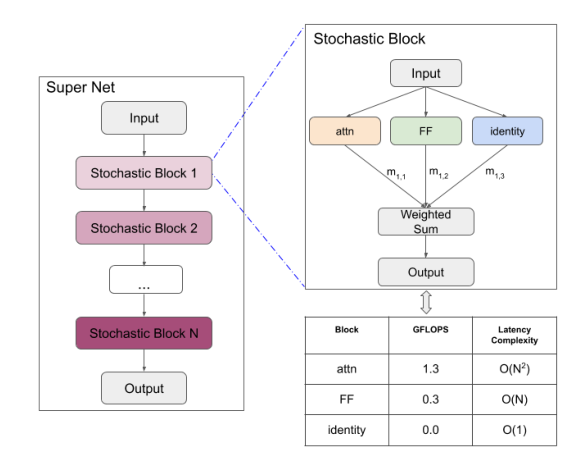
Without the constraint that the linear combination coefficients being a probability distribution (i.e. in [0,1] and summing to 1), this is trivially solved by using a nn.Linear(N, 1) layer on the torch.stacked outputs, but i think that would not be really useful to my task: I would probably see some negative coefficients, and I wouldn’t know what to make of them. I could visualize a softmax of the coefficient, but it would have nothing to do with the actual parameters.
So I hacked together this code which seems to be doing it by re-assigning the Linear weights at every step to their softmax; i’m not even sure this would make sense.
class MultiLayer(nn.Module):
''' Utility class to get outputs from N modules '''
def __init__(self, *modules):
super().__init__()
self.layers = nn.ModuleList(modules)
def forward(self, x, mask = None):
return [
layer(x) if not 'attention' in layer.__class__.__name__
else layer(x, mask=mask)
for layer in self.layers
]
class LinearComb(nn.Module):
def __init__(self, *modules):
super().__init__()
n = len(modules)
assert n >= 2, 'Pointless use of this class'
self.nets = MultiLayer(*modules)
self.coefficients = nn.Linear(n, 1, bias=False)
torch.nn.init.xavier_uniform_(self.coefficients.weight.data)
def forward(self, x, mask = None):
# turn weights into probability distribution
self.coefficients.weight.data = torch.nn.functional.gumbel_softmax(
self.coefficients.weight.data, dim = 0
)
# get tensor from modules outputs
module_outs = torch.stack(
self.nets(x, mask),
dim=-1
)
# compute linear combination
return self.coefficients(module_outs).squeeze(-1)
Does somebody know if this is a viable solution or if it could hurt model performance in any way? Again, my final goal is just to get a weighted sum of N tensors, where the weights are a probability distribution (specifically, the paper’s authors are talking about weights sampled from a Gumbel softmax distribution. I’m not even sure i’m using it correctly)