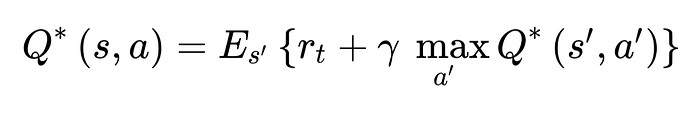The loss does keep increasing when I set lr=0. While it is predictable since in each epoch, if we suppose that the NN keeps output F=0, then the angle (y) will keeps increasing by each timestamp. The whole system is like the pic below, where angle (y) represents the angle of the pole and F is the force applied on the cart.
The loss does keep increasing when I set
lr=0.
Does this explain the problem or does the loss still increase unexpectedly much when you set lr = 0.001?
well this doesn’t explain the problem since the loss never decreases during the training.
I tried to set lr=10000000, the changing of outputs of the NN still look similar to when lr=0.001 is used.
I ran your code. The issue is the way you are calculating the loss increases as the pendulum swings further off course, which, of course, will happen during initial training. Your function y= ( old_x + (torch.mm(A,old_x)+torch.mm(B,F))*interval_step_ ) ensures this happens as the model goes way off course, which it will be initially. And that can be a major problem for training as the current setup will magnify the decisions made when it’s definitely falling and minimize the decisions made when it’s nearly upright. The Q function in DQN helps to normalize that over the entire time.
Tinkered with your code a bit and got it working, albeit with some major changes:
- The loss function is now CrossEntropyLoss and the model gives two outputs, depicting the direction of the force to be applied, the magnitude is a fixed value.
- Parallelized the games so you can have batches going at a time.
- Added a greedy epsilon function(although, it might not be necessary in this case).
After these changes, not only does the loss decline but the pendulum can stay upright in excess of 20 seconds. I didn’t test how long it could go.
import matplotlib.pyplot as plt
import numpy as np
import time
from matplotlib.animation import FuncAnimation
import torch
from torch import nn
#------------------------------------------------------------------------- Define model
class NeuralNetwork(nn.Module):
def __init__(self, n1=32):
super().__init__()
self.linear_relu_stack = nn.Sequential(
nn.Linear(4, n1),
nn.ReLU(),
nn.Linear(n1,n1),
nn.ReLU(),
nn.Linear(n1, 2)
)
def forward(self, x):
x = x.reshape((-1,4))
logits = self.linear_relu_stack(x)
return logits
batch_size=1200
def get_greedy_action(size):
return torch.randn((size,1))*10
def train(model, loss_fn, optimizer, epsilon):
# total simulation time interval /seconds
t_time = 20
# time interval of each step /seconds
interval_step = 0.01
force_mult=4.0
# total simulation loop numbers
loop = int(t_time / interval_step)
# print(loop)
alpha=6
model.train()
A = np.array([[0, 1, 0, 0], [15.244, 0, 0, 0], [0, 0, 0, 1], [-0.363, 0, 0, 0]])
A=torch.tensor(A,dtype=torch.float32)
B = np.array([[0], [-0.741], [0], [0.494]])
B = torch.tensor(B, dtype=torch.float32)
#x_init = np.array([[round(np.random.uniform(-1, 1), 3) * 10], [0], [0], [0]])
x = torch.cat([torch.randn((batch_size, 1))*10, torch.zeros((batch_size,3))], dim=1)
total_loss=0
done=torch.zeros(batch_size, dtype=torch.bool)
F_list=[]
#start simulation loop
for i in range(loop):
#x'=Ax+Bu
F = model(x[~done,...])
greedy=torch.rand(F.size(0))<epsilon
F[greedy] = torch.rand_like(F.detach())[greedy]
F_list.append(F)
G=torch.argmax(F.clone().detach(), dim=1).view(-1,1)
Gzero=G==0
G[Gzero]=-1
G=G*force_mult
interval_step_=torch.tensor(interval_step)
y= ( x[~done,...] + (A@x[~done,...].T+B@G.T).T*interval_step_ )
leftmask=y[:,0:1]>0
x[~done,...]=y.detach()
#k=torch.cat([torch.ones(batch_size,1), torch.zeros(batch_size, 3)], dim=1).float()
#y=(k@y.T).T
targs=leftmask.long()
loss = loss_fn(F,targs.view(-1))
#loss/=((i+1)*alpha)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss+= loss.item()
#print(f"loss: {loss:>7f}")
done=torch.abs(x[:,0:1])>25
done=done.view(-1)
if torch.sum(done)>batch_size-batch_size//100:
break
total_loss=total_loss/((i+1))
tstep=i*interval_step
if tstep>1.5:
print("control fail in %.2f seconds" %tstep, "| Loss was %.3f" %total_loss)
#-------------------------------------------------------------------------------define simulation and training in each epoch
model=NeuralNetwork()
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.0001, momentum=0.9, nesterov=True)
epochs = 10000
epsilon = 0.995
min_ep=0.001
for e in range(epochs):
train(model, loss_fn, optimizer, epsilon)
if epsilon>min_ep:
epsilon*=(100-e)/100
Cheers.
cheers!This is really amazing and i really appreciate your help.
Actually I am learning DQN and try to find a solution. Well it is kinda difficult for me.
In your code, it is changed to a classification problem. I see that the label value of each F comes from leftmask=y[:,0:1]>0. Does it mean if the angle at the next timestamp is larger than zero, then the label value of previous F should be 1(positive direction)? I am a little confused about the meaning behind it.
Right. It turns into into a simple choice of direction.
That function creates a True/False statement, which .long() turns into 0s and 1s. I.e. if it’s angle is negative, the correct choice would have been positive, and vice versa.
You could probably do the same thing for the targets with the previous x value. Actually, that might be more appropriate.
Yeah, if in the current state, the angle is negative, then the label value of F should be positive, since we want it to stay upright. This do sound more appropriate.
Well I think in my original code, I try to train the NN in an “unusual” supervised learning style, while actually it may be wrong. The problem is close to a RL problem and DQN (I am working on it) can be a good solution. However, do you think by any chance that we can do some improvement to solve the problem by using a NN that output the force F without using DQN?
I stated that wrong earlier. Positive force for positive angle and vice versa. The code is correct, though.
You could try the inverse function to get the needed force for the angle to be zero + state.
Okay, thanks. I guess a direct label value is always required for the supervised training of a NN.
By the way, this code I posted earlier technically does not making use of Bellman’s Q Learning optimality equation.
As this implementation applies a reward at each timestep without making use of discounted rewards across timesteps. TBH, not really sure what it falls under.
So while it might work well on this particular problem - fixing the force applied to a given quantity - it might not work on other problems that do not make use of variable discrete timesteps. The Pytorch DQN tutorial referenced earlier makes use of an actual Q Learning function.