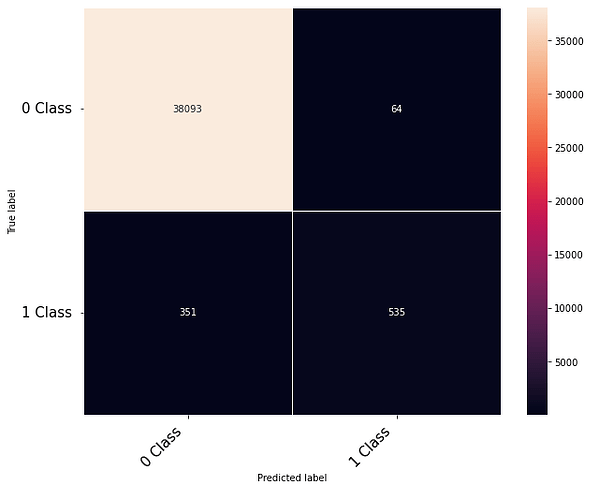
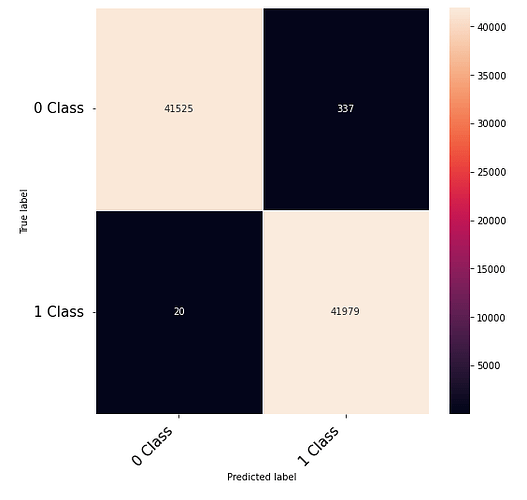
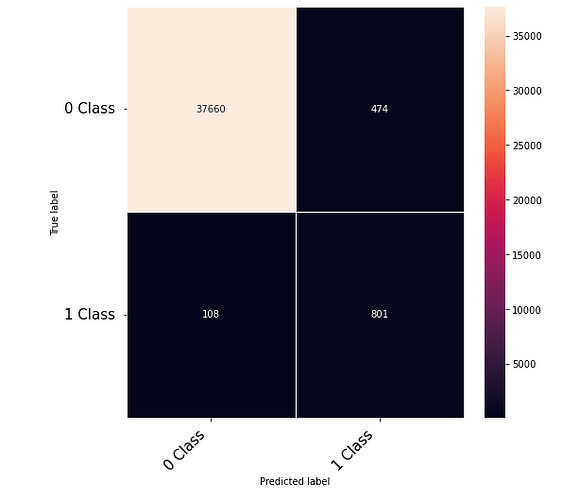
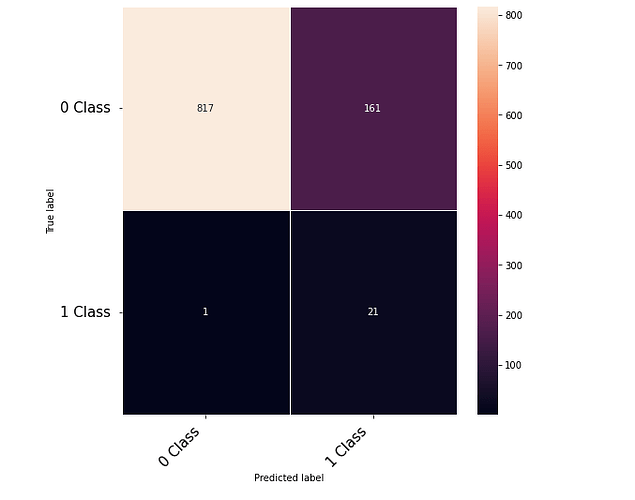
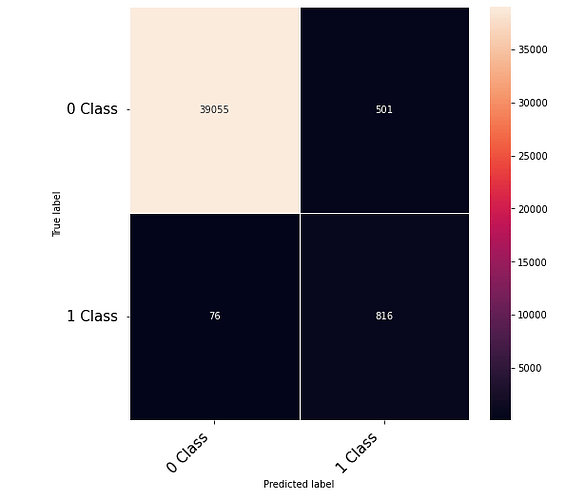
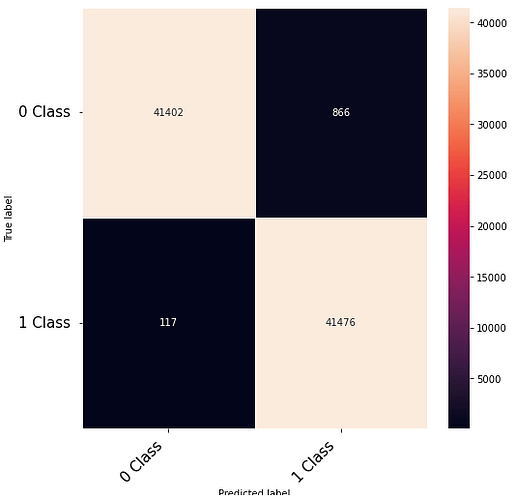Hi Community,
Thanks to the posts within this community. The following code that takes numerical inputs that are 1 x 6156 (in the range of 0 to 1) and classifies them in 2 classes [0 or 1]. With a 10 layer network I was about to get to a low loss (0.000089) but the test data gives a 60% on the F-1 score. Previous architecture had a loss of 0.002 with an F-1 score of 68%. This is counter intuitive as to why the lower loss architecture did worse. Other posts say it could be something in the code — is it possible I am doing something wrong in the testing or training?
Hope this code can also help others that don’t deal with images !
Side note: for the forward, only having the sigmoid in the first layer gave the lowest loss. I tried all other variations and it worsen the training.
X_train,X_test,y_train,y_test = train_test_split(Concatenated_x,Concatenated_y,random_state = 28,test_size=0.3151)
from torch.utils.data import Dataset, DataLoader
class Data(Dataset):
def __init__(self, X_train, y_train):
self.X = torch.from_numpy(X_train.astype(np.float32))
self.y = torch.from_numpy(y_train).type(torch.LongTensor)
self.len = self.X.shape[0]
def __getitem__(self, index):
return self.X[index], self.y[index]
def __len__(self):
return self.len
traindata = Data(np.asarray(X_train), np.asarray(y_train))
trainloader = DataLoader(traindata, batch_size=batch_size,shuffle=True, num_workers=0)
import torch.nn as nn
input_dim = 6156 #
hidden_layers = 12312
hidden_layers2 = 6156
hidden_layers3 = 3078
hidden_layers4 = 1539
hidden_layers5 = 770
hidden_layers6 = 385
hidden_layers7 = 192
hidden_layers8 = 96
hidden_layers9 = 48
hidden_layers10 = 24
output_dim = 2
class Network(nn.Module):
def __init__(self):
super(Network, self).__init__()
self.linear1 = nn.Linear(input_dim, hidden_layers)
self.linear2 = nn.Linear(hidden_layers, hidden_layers2)
self.linear3 = nn.Linear(hidden_layers2, hidden_layers3)
self.linear4 = nn.Linear(hidden_layers3, hidden_layers4)
self.linear5 = nn.Linear(hidden_layers4, hidden_layers5)
self.linear6 = nn.Linear(hidden_layers5, hidden_layers6)
self.linear7 = nn.Linear(hidden_layers6, hidden_layers7)
self.linear8 = nn.Linear(hidden_layers7, hidden_layers8)
self.linear9 = nn.Linear(hidden_layers8, hidden_layers9)
self.linear10 = nn.Linear(hidden_layers9, hidden_layers10)
self.linear11 = nn.Linear(hidden_layers10, output_dim )
def forward(self, x):
x = torch.sigmoid(self.linear1(x)) #original
x = (self.linear2(x))
x = (self.linear3(x))
x = (self.linear4(x))
x = (self.linear5(x))
x = (self.linear6(x))
x = (self.linear7(x))
x = (self.linear8(x))
x = (self.linear9(x))
x = (self.linear10(x))
x = (self.linear11(x))
return x
valid_loss_min = np.Inf
path = "Model_1.pth"
clf.train()
for epoch in range(epochs):
print("Epoch-----"+str(epoch)+"------Running")
running_loss = 0.0
loss_values = []
for i, data in enumerate(trainloader, 0):
# get the inputs; data is a list of [inputs, labels]
inputs, labels = data[0].to(device), data[1].to(device)
# inputs, labels = data
# Clear the gradients
optimizer.zero_grad()
# Forward Pass
outputs = clf(inputs)
_, preds = torch.max(outputs, 1)
labels = labels.squeeze_()
# Find the Loss
loss = criterion(outputs, labels)
# Calculate Gradients
loss.backward()
# Update Weights
optimizer.step()
# Calculate Loss
running_loss += loss.item() * inputs.size(0) # Loss of batch
# print(f'[{epoch + 1}, {i + 1:5d}] loss: {running_loss / len(traindata):.5f}') # Original
print('epoch {}, loss {:.6f}'.format(epoch, loss.item()))
## save the model if validation loss has decreased
if loss <= valid_loss_min:
print('Validation loss decreased ({:.6f} --> {:.6f}). Saving model..'.format(valid_loss_min, loss))
torch.save(clf.state_dict(), path)
print('Model Saved')
Now for the testing code, it’s as follows:
clf.load_state_dict(torch.load(path))
clf.eval() # set the dropout and batch normalization layers to evaluation mode
testdata = Data(np.asarray(X_test), np.asarray(y_test))
testloader = DataLoader(testdata, batch_size=batch_size,
shuffle=False, num_workers=0)
dataiter = iter(testloader)
inputs, labels = dataiter.next()
print(inputs)
print(labels)
outputs = clf(inputs) # The outputs are energies for the 2 classes, higher energy, the more the network thinks its a class
__, predicted = torch.max(outputs, 1) # get the index of the highest energy
print(predicted)
nb_classes = 2
from sklearn.metrics import precision_recall_fscore_support as score
confusion_matrix = torch.zeros(nb_classes, nb_classes)
with torch.no_grad():
for i, (inputs, classes) in enumerate(testloader):
inputs = inputs
classes = classes
outputs = clf(inputs)
_, preds = torch.max(outputs, 1)
for t, p in zip(classes.view(-1), preds.view(-1)):
confusion_matrix[t.long(), p.long()] += 1
cm = confusion_matrix.cpu().data.numpy()
recall = np.diag(cm) / np.sum(cm, axis = 1)
precision = np.diag(cm) / np.sum(cm, axis = 0)
print(confusion_matrix)
print(confusion_matrix.diag()/confusion_matrix.sum(1))