Hi,
I have a question about implementation of masking in Transformer decoders. I understand that the purpose of masking is so we dont peek at future tokens in the target sequence.
I am trying to understand why the subsequent tokens that are masked are filled with -inf rather than 0s. https://github.com/pytorch/pytorch/blob/master/torch/nn/functional.py#L3427
I imagined that these positions would be filled with 0s so that when dot product is taken, then corresponding future positions would be 0, and so would the gradient. And then there would be no change in parameters in the corresponding future positions when we take a step along the gradient. With the -inf I think the gradients would be -inf/ill-defined? And the resulting solution would have nans in the subsequent positions.
Could you please help me understand the reasoning for filling with -inf?
Thanks!
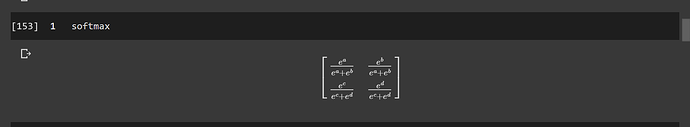



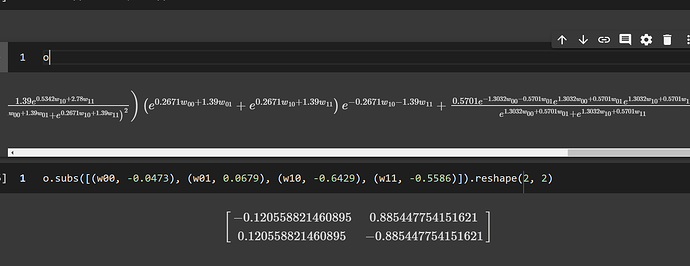
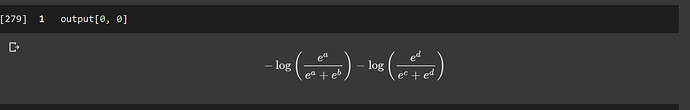
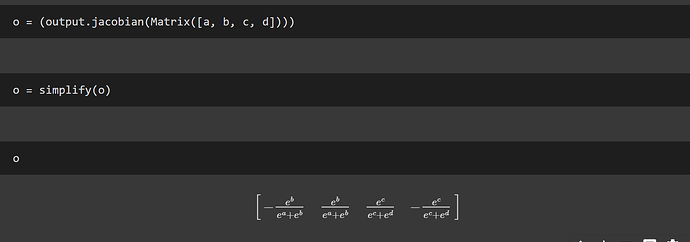

 May I ask what software/package you used for the symbolic representation in your screenshots? Can you do that with pytorch?
May I ask what software/package you used for the symbolic representation in your screenshots? Can you do that with pytorch?