Matmul operation does not benefit from larger batch size

[Louka_Ewington-Pitso (Louka Ewington-Pitsos)]

I am performing a simple matrix multiplication via pytorch/cuda on a 16 GB GPU. I am doing this multiple times until i cover 1024 samples.

when I increase the batch size, the overall time to execute does not decrease. Here is the code to reproduce

import time
import torch

n = 768
weight = torch.randn(768, n, dtype=torch.float32, device='cuda')


results = []
bss = [64, 32, 16, 8, 4, 2] 
for bs in bss:
    q = torch.empty(bs, 1024, 768, dtype=torch.float32, device='cuda')
    torch.cuda.synchronize()
    start = time.time()
    torch.cuda.synchronize()
    with torch.no_grad():
        for i in range(0, 1024, bs):
            a = (q @ weight)
    torch.cuda.synchronize()
    end = time.time()
    elapsed = end - start
    results.append(elapsed)
    print(f'bs={bs}, elapsed={elapsed}')

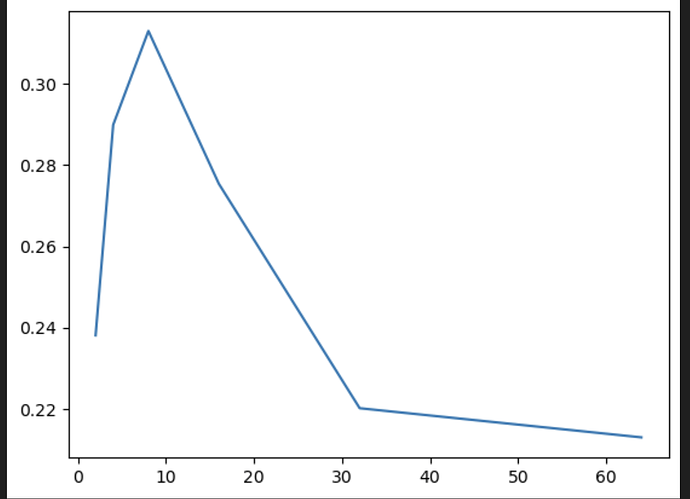
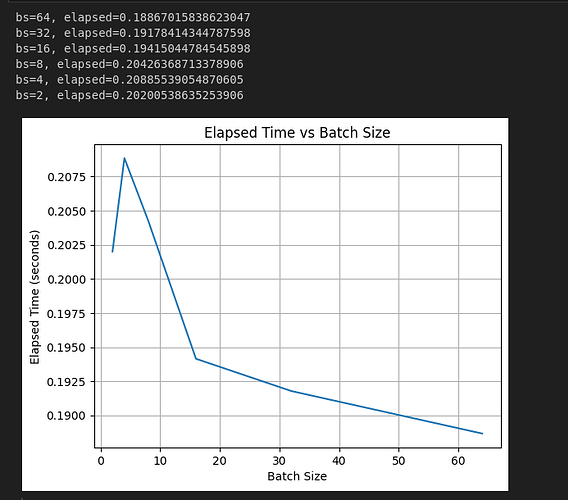
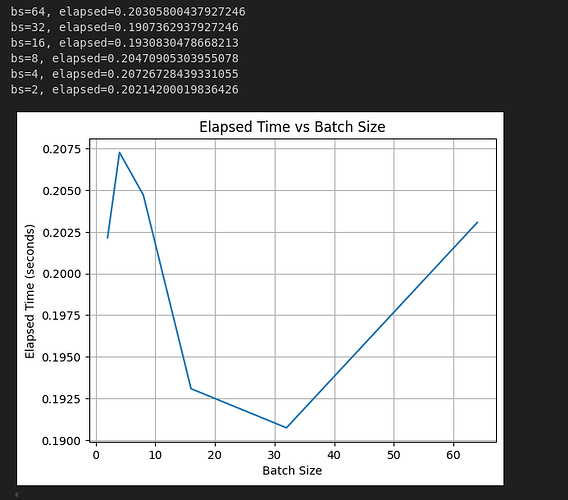
This is the output

bs=64, elapsed=0.2129044532775879
bs=32, elapsed=0.2200911045074463
bs=16, elapsed=0.2754323482513428
bs=8, elapsed=0.31310248374938965
bs=4, elapsed=0.289961576461792
bs=2, elapsed=0.23805022239685059

I would have thought that the the execution time should roughly halve each time we double the batch size.

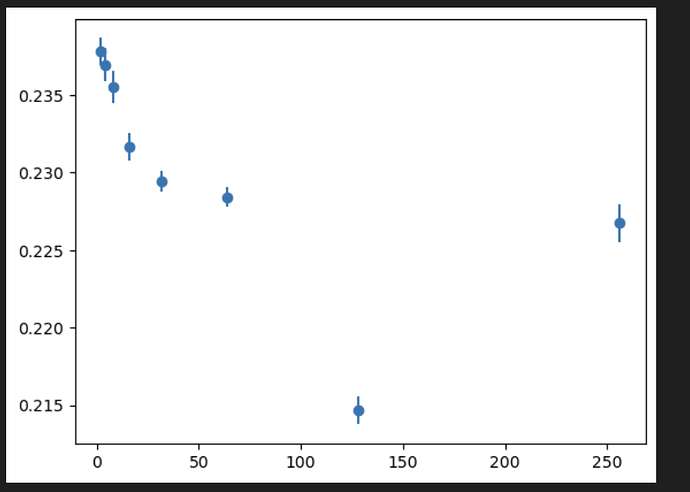
I also try with different matrix sizes

# at n = 64
bs=256, elapsed=0.029320716857910156
bs=128, elapsed=0.02939009666442871
bs=64, elapsed=0.02989816665649414
bs=32, elapsed=0.03046727180480957
bs=16, elapsed=0.0326845645904541
bs=8, elapsed=0.03428316116333008
bs=4, elapsed=0.036544084548950195
bs=2, elapsed=0.03979301452636719


at n = 16384
bs=64, elapsed=5.368429660797119
bs=32, elapsed=4.477093935012817
bs=16, elapsed=4.486705780029297
bs=8, elapsed=7.2721076011657715
bs=4, elapsed=7.306727170944214
bs=2, elapsed=7.336323261260986

I thought matrix multiplication was like, the perfect example of an operation which should benefit from larger batch sizes.

Here is my nvidia-smi

+---------------------------------------------------------------------------------------+
| NVIDIA-SMI 535.183.01             Driver Version: 535.183.01   CUDA Version: 12.2     |
|-----------------------------------------+----------------------+----------------------+
| GPU  Name                 Persistence-M | Bus-Id        Disp.A | Volatile Uncorr. ECC |
| Fan  Temp   Perf          Pwr:Usage/Cap |         Memory-Usage | GPU-Util  Compute M. |
|                                         |                      |               MIG M. |
|=========================================+======================+======================|
|   0  Tesla T4                       On  | 00000000:00:1E.0 Off |                    0 |
| N/A   34C    P0              33W /  70W |      2MiB / 15360MiB |      0%      Default |
|                                         |                      |                  N/A |
+-----------------------------------------+----------------------+----------------------+
                                                                                         
+---------------------------------------------------------------------------------------+
| Processes:                                                                            |
|  GPU   GI   CI        PID   Type   Process name                            GPU Memory |
|        ID   ID                                                             Usage      |
|=======================================================================================|
|  No running processes found                                                           |
+---------------------------------------------------------------------------------------+

Perhaps my profiling is just wrong, I would love to know what is going on here.

[Tahamustapha_Nehdi]

Hi louka

Actually, there are several matrix multiplication functions in PyTorch

AB = A.mm(B)

AB = torch.mm(A, B)

AB = torch.matmul(A, B)

AB = A @ B  # Python 3.5+ only

There are a few subtleties.

`torch.mm` does not broadcast. For broadcasting matrix products, see `torch.matmul()` .

trying torch.matul in your code will give this curve

but " @ " gives this curve

[Louka_Ewington-Pitso (Louka Ewington-Pitsos)]

@Tahamustapha_Nehdi thank you, its good to know the different operations make a difference

Still though a speed increase of 0.05 seconds for increasing the batch size from 16 to 64 seems like we’re not really gaining much parallelism benefits here.

[Louka_Ewington-Pitso (Louka Ewington-Pitsos)]

Perhaps this article is relevant: GPU Memory Size and Deep Learning Performance (batch size) 12GB vs 32GB -- 1080Ti vs Titan V vs GV100 | Puget Systems

In the article it seems that often increasing the batch size increases training throughput significantly until you reach a certain level of saturation, after which further increases to the batch size only have a small impact.

The article was profiling the full ML training loop though including backprop.

[AlphaBetaGamma96]

Hi,

When measuring the time I think it’s good practice to make sure to ‘warm-up’ and measure the function a few times to gather decent statistics of how fast a particular function is working.

Here’s an example script,

import torch
from torch.func import vmap
from time import perf_counter
from torch import compile #can compile the function as well

n = 768
weight = torch.randn(768, n, dtype=torch.float32, device='cuda')

def measure_time_with_sync():
	torch.cuda.synchronize()
	return perf_counter()

warm_up=10
n_repeats=11

#Diff. methods to compute a 'batched'-matmul

def broadcast_matmul(a,b):
	return a @ b

def vmapped_matmul(a,b):
	return vmap(torch.matmul, in_dims=(0, None))(a, b)

def einsum_matmul(a,b):
	return torch.einsum('...ij,jk->...ik',a,b)

#Uncomment one function to test.

func = broadcast_matmul
#func = vmapped_matmul
#func = einsum_matmul

print('Function: ',func.__name__)

results = []
batch_sizes=[512, 256, 128, 64, 32, 16, 8, 4, 2] #higher batch sizes
for batch_size in batch_sizes:
	q = torch.randn(batch_size, 1024, 768, dtype=torch.float32, device='cuda')
	times = []

	for _ in range(warm_up): #warm up our function
		func(q, weight)
		
	for _ in range(n_repeats): #repeat a few times for decent stats.
		start = measure_time_with_sync()	
		func(q, weight)
		end = measure_time_with_sync()
		elapsed = end - start
		times.append(elapsed)
	
	times = torch.as_tensor(times)
	mean = torch.mean(times)
	std = torch.std(times)

	print(f'batch_size: {batch_size} | Walltime: {mean:.2e}s +/- {std:.2e}s')

This script produces the following results for me,

Function:  broadcast_matmul
batch_size: 512 | Walltime: 1.52e-01s +/- 1.06e-02s
batch_size: 256 | Walltime: 7.09e-02s +/- 6.12e-04s
batch_size: 128 | Walltime: 4.07e-02s +/- 1.26e-03s
batch_size: 64  | Walltime: 1.76e-02s +/- 5.06e-04s
batch_size: 32  | Walltime: 8.84e-03s +/- 2.10e-04s
batch_size: 16  | Walltime: 4.42e-03s +/- 4.10e-05s
batch_size: 8   | Walltime: 2.33e-03s +/- 2.21e-04s
batch_size: 4   |  Walltime: 1.14e-03s +/- 8.80e-05s
batch_size: 2   | Walltime: 5.71e-04s +/- 6.33e-06s

Function:  vmapped_matmul
batch_size: 512 | Walltime: 1.42e-01s +/- 1.02e-03s
batch_size: 256 | Walltime: 7.11e-02s +/- 4.24e-04s
batch_size: 128 | Walltime: 3.58e-02s +/- 3.10e-04s
batch_size: 64  | Walltime: 1.78e-02s +/- 1.44e-04s
batch_size: 32  | Walltime: 8.81e-03s +/- 6.67e-05s
batch_size: 16  | Walltime: 4.44e-03s +/- 5.86e-05s
batch_size: 8   | Walltime: 2.38e-03s +/- 2.81e-04s
batch_size: 4   | Walltime: 1.19e-03s +/- 9.46e-05s
batch_size: 2   | Walltime: 6.21e-04s +/- 5.73e-06s

Function:  einsum_matmul
batch_size: 512 | Walltime: 1.43e-01s +/- 1.91e-03s
batch_size: 256 | Walltime: 7.14e-02s +/- 4.62e-04s
batch_size: 128 | Walltime: 3.58e-02s +/- 3.99e-04s
batch_size: 64  | Walltime: 1.79e-02s +/- 1.81e-04s
batch_size: 32  | Walltime: 8.87e-03s +/- 3.59e-04s
batch_size: 16  | Walltime: 4.43e-03s +/- 6.09e-05s
batch_size: 8   | Walltime: 2.34e-03s +/- 2.84e-04s
batch_size: 4   | Walltime: 1.14e-03s +/- 9.80e-05s
batch_size: 2   | Walltime: 5.79e-04s +/- 2.50e-06s

[Louka_Ewington-Pitso (Louka Ewington-Pitsos)]

Thanks for the great advice @AlphaBetaGamma96

It looks like you are observing the same thing as me, i.e. that the time to execute increases in a roughly linear fashion with batch size, meaning there is little if any performance gain from using a larger batch size.

using your advice I re-write my initial script to include warm-up and mean/std calculations. I feel like this is much better practice, but the results ended up being more or less the same (very small difference between batch size of 2 vs 256).

import time
import torch
import matplotlib.pyplot as plt
import numpy as np

n = 768
weight = torch.randn(768, n, dtype=torch.float32, device='cuda')

warm_up = 25
tries = 15

results_mean = []
results_std = []
bss = [256, 128, 64, 32, 16, 8, 4, 2] 
for bs in bss:
    trials = []
    q = torch.empty(bs, 1024, 768, dtype=torch.float32, device='cuda')

    for _ in range(warm_up):
        a = q @ weight

    for _ in range(tries):
        torch.cuda.synchronize()
        start = time.time()

        with torch.no_grad():
            for i in range(0, 1024, bs):
                a = q @ weight

        torch.cuda.synchronize()
        end = time.time()
        elapsed = end - start
        trials.append(elapsed)
    results_mean.append(np.mean(trials))
    results_std.append(np.std(trials))
    print(f'bs={bs}, elapsed={elapsed}')