Mismatched output size when using convolution layer [Figure]

1

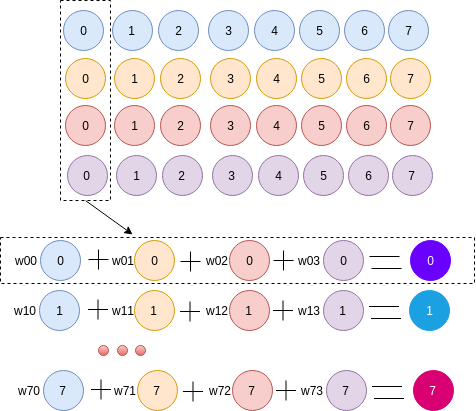
I have four vectors size of 1x8. I want to a new vector where each element row of the new vector is a linear combination of each element row in the four vectors as the figure. The expected output should be 1x8.

My solution is that using convolution to learn the weight. I convert the vector size of 1x8 to BxCxHxW, where W=1, and H=8, C is the number of vector. The combined vector has the size of 1x4x8x1. Now, we can use traditional conv2d with input size of 1x4x8x1 to produce the output size of 1x1x8x1. However, the output size (1x1x7x1) is mismatched with my expected. How should I solve it? How do you think my implementation of the problem. Is it kernel size = (4x1) or (1x1)?
Untitled%20Diagram

import torch
import torch.nn as nn
class learn_vector(nn.Module):
    def __init__(self, in_channels, out_channels):
        super(learn_vector, self).__init__()
        self.conv = nn.Conv2d(in_channels, 1, kernel_size=(in_channels, 1), stride=1, padding=(1,0), bias=True)

    def forward(self, x):
        print(x.size())
        x = self.conv(x)
        return x

batch_size, channel = 1, 8
input_vec1 = torch.randint(1, 100, (batch_size,channel)) # [1, 8]
input_vec2 = torch.randint(1, 100, (batch_size,channel)) # [1, 8]
input_vec3 = torch.randint(1, 100, (batch_size,channel)) # [1, 8]
input_vec4 = torch.randint(1, 100, (batch_size,channel)) # [1, 8]
# Extend vector from BxC --> BxC1xDxHxW where C=D
input_vec1 = input_vec1.view(batch_size, 1, channel, 1)
input_vec2 = input_vec2.view(batch_size, 1, channel, 1)
input_vec3 = input_vec3.view(batch_size, 1, channel, 1)
input_vec4 = input_vec4.view(batch_size, 1, channel, 1)
# Concat these vectors
input_concat = torch.cat([input_vec1, input_vec2, input_vec3, input_vec4], 1) #torch.Size([1, 4, 8, 1])
input_concat = input_concat.float()
# Feed to the network
learn_net = learn_vector(input_concat.size(1), 1)
out = learn_net(input_concat)
out = out.transpose (1,2)  #torch.Size([1, 7, 1, 1])
print (out.size())
2

Your kernels currently use all 4 input channels, which is fine, but also have a kernel size of (4, 1), which is probably not what you want.
The kernel will not only use all channels (different colors), but also use 4 values in one spatial dimension (e.g. values 0, 1, 2, 3).

In your use case, you could use nn.Conv1d with 4 input channels and a kernel size of 1 or alternatively just a linear layer.
Here is a small example:

batch_size, channel = 1, 8
input_vec1 = torch.randint(1, 100, (batch_size,channel)) # [1, 8]
input_vec2 = torch.randint(1, 100, (batch_size,channel)) # [1, 8]
input_vec3 = torch.randint(1, 100, (batch_size,channel)) # [1, 8]
input_vec4 = torch.randint(1, 100, (batch_size,channel)) # [1, 8]
# Extend vector from BxC --> BxC1xDxHxW where C=D
input_vec1 = input_vec1.view(batch_size, 1, channel)
input_vec2 = input_vec2.view(batch_size, 1, channel)
input_vec3 = input_vec3.view(batch_size, 1, channel)
input_vec4 = input_vec4.view(batch_size, 1, channel)
# Concat these vectors
input_concat = torch.cat([input_vec1, input_vec2, input_vec3, input_vec4], 1) #torch.Size([1, 4, 8, 1])
input_concat = input_concat.float()
# Feed to the network
conv = nn.Conv1d(4, 1, 1, 1, 0)
out = conv(input_concat)
print (out.size())

lin = nn.Linear(4, 1)
with torch.no_grad():
    lin.weight = nn.Parameter(conv.weight.squeeze(2))
    lin.bias = nn.Parameter(conv.bias)
out_lin = lin(input_concat.permute(0, 2, 1))

torch.allclose(out_lin.squeeze(), out.squeeze())
1 Like
3

The kernel will not only use all channels (different colors), but also use 4 values in one spatial dimension (e.g. values 0, 1, 2, 3).

Thanks so much. So, I have to use same weight for all position (position 0 to position 7). Is it right? Because my aim is find a linear combination of all vectors column by column. So, I expect to have different weights among columns. For example, (w00, w01,w02, w03) is for first column must be different with (w10, w11,w12, w13) of second column and so on. Is it possible?

4

Oh, I clearly misunderstood your use case, sorry!
I thought the kernel would be the dotted line in your figure, but I’ve apparently didn’t read the indices carefully enough.

So basically you have a weight for each input value. Both of my approaches use some kind of weight sharing and are not doing what you are trying to achieve.

In that case you could use nn.Conv1 with a kernel size of 4 and groups=in_channels, where in_channels is now 8.

From the docs:

At groups= in_channels , each input channel is convolved with its own set of filters (of size ⌊out_channels / in_channels⌋).

input_concat = input_concat.permute(0, 2, 1)
print(input_concat.shape)  # [1, 8, 4]
conv = nn.Conv1d(
    in_channels=8,
    out_channels=8,
    kernel_size=4,
    padding=0,
    groups=8
)
out = conv(input_concat)
1 Like
5

I so appreciate your solution. It makes me more clear about the purpose of group convolution. In summary, we have a input size of 1x8x4, where 1 is batch size, 8 is row and 4 is column. An output vector with size of 1x8x1, in which each row in the new vector is a linear combination (with an own weight set) of 4 columns in the input vector. We solve it using convolution 1d with group size of number row. Am I correct?

6

Yes, your explanation is right!
Just a small side note: the rows and columns correspond to channels and sequence length, respectively.

7

@ptrblck: It worked. I just want to make more clear by using your second way. It used linear operator. So, instead of using 1 linear, we will use 8 linear operators (corresponding to 8 neurons or length). So, it will be

lin0 = nn.Linear(4, 1) # for first linear of zeros's combination
lin1 = nn.Linear(4, 1) # for first linear of ones's combination
...
lin7 = nn.Linear(4, 1) # for first linear of eights's combination
with torch.no_grad():
    lin0.weight = nn.Parameter(conv.weight.squeeze(2))
    lin0.bias = nn.Parameter(conv.bias)
    lin1.weight = nn.Parameter(conv.weight.squeeze(2))
    lin1.bias = nn.Parameter(conv.bias)
    ...

input_concat = input_concat.permute(0, 2, 1)
out_lin0 = lin0(input_concat[:,:,0])  # w00 O0 + w01 O1 + w02 O2 + w03 O3
out_lin1 = lin1(input_concat[:,:,1])
...

How do you think that? Is it correct?

8

Generally yes, this approach should output the same values as the grouped convolutions.
However, currently you are assigning the complete conv weight parameter to each linear layer.
This code should work:

lins = [nn.Linear(4, 1) for _ in range(8)]
with torch.no_grad():
    for idx, lin in enumerate(lins):
        lin.weight = nn.Parameter(conv.weight[idx])
        lin.bias = nn.Parameter(conv.bias[idx].unsqueeze(0))
    
outputs = torch.stack([lin(input_concat[:, idx]) for idx, lin in enumerate(lins)], 1)
print(torch.allclose(outputs, out))
> True
9

In the training, Do I need to use these lines:

with torch.no_grad():
    for idx, lin in enumerate(lins):
        lin.weight = nn.Parameter(conv.weight[idx])
        lin.bias = nn.Parameter(conv.bias[idx].unsqueeze(0))

Or you just make it to check the output of convolution and linear are equally. Finally, the training just use

lins = [nn.Linear(4, 1) for _ in range(8)]
outputs = torch.stack([lin(input_concat[:, idx]) for idx, lin in enumerate(lins)], 1)
10

I just used it to check both outputs for equality. If you would like to use the linear layer approach, you won’t need the grouped convolutions.

1 Like
11

Great to know a new approach for comparsion. What do you think which one is faster, linear or conv1d for training and testing if the number of node is 512? Thanks

12

512 is the number of channels, i.e. also the number of linear layers?
The for loop might slow down the linear approach, so I guess the conv approach would be faster, but to be sure I would just time them in a small function using random input.
Remember to use torch.cuda.synchronize() before starting and stopping the timer, if you want to compare both approaches on the GPU.

13

Thanks, It worked now using linear operators. However, I would like to note that, if the module is incorporated in the network, it has to add .cuda or to(device) that is a difference with other operators likes conv, softmax, sigmod, batchnorm…It means we have to change nn.Linear(4, 1) to nn.Linear(4, 1).cuda() in the __init__ function alothugh I have used learn_vector().cuda() before. I am using pythorch version 1.0.

import torch
import torch.nn as nn
class learn_vector(nn.Module):
    def __init__(self, in_channels, out_channels):
        super(learn_vector, self).__init__()
        lins = [nn.Linear(4, 1).cuda() for _ in range(8)]
    def forward(self, x):
        print(x.size())
        outputs = torch.stack([lin(x[:, idx]) for idx, lin in enumerate(lins)], 1)
        return outputs
14

If you are using lins inside a nn.Module you should use nn.ModuleList instead of a plain Python list to properly register all linear layers. Otherwise e.g. the optimizer won’t be able to find them.
This will also make sure to transfer all layers onto your GPU, if you call lean_vector.cuda().

15

You mean lins = [nn.Linear(4, 1).cuda() for _ in range(8)] to

self.lins = nn.ModuleList([])
for i in range (8): 
   lins.append(nn.Linear(4, 1))

Am I correct?

16

You can just wrap the list comprehension into nn.ModuleList:

class learn_vector(nn.Module):
    def __init__(self, in_channels, out_channels):
        super(learn_vector, self).__init__()
        self.lins = nn.ModuleList([nn.Linear(4, 1) for _ in range(8)])
    def forward(self, x):
        print(x.size())
        outputs = torch.stack([lin(x[:, idx]) for idx, lin in enumerate(self.lins)], 1)
        return outputs

Also, you forgot to register lins as class attributes using self.
Using this code, you can now create the model and push it onto the device:

model = learn_vector(1, 1).to('cuda')
1 Like