Hello,
I’m trying to get a mixture density network to approximate multivariate distributions. As a pedagogic, toy-example, I’m considering a noisy linear distribution.

As a baseline, I’m fitting this with a basic model:
baseline = nn.Sequential(nn.Linear(1,32), nn.ReLU(), nn.Linear(32,1))
Which allows me to get:
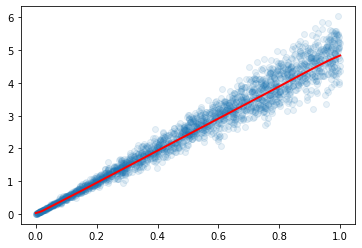
Now, I’m creating a mixture model as such:
class MixtureModel(nn.Module):
def __init__(self, k = 5):
super().__init__()
self.base = nn.Sequential(nn.Linear(1,128),
nn.ReLU(),
nn.Linear(128,128),
nn.ReLU())
self.means = nn.Linear(128,k)
self.stds = nn.Linear(128,k)
self.weights = nn.Linear(128,k)
def forward(self, x):
latent = self.base(x)
means = self.means(latent)
stds = F.elu(self.stds(latent)) + 1
w = F.softmax(self.weights(latent), dim = 1)
return means, stds, w
Training goes like this, maximizing log likelihood of observed data:
model = MixtureModel()
adam = optim.Adam(model.parameters(), lr = 1e-2)
loader = DataLoader(DS(), batch_size = 64, shuffle = True)
epochs = 50
losses = []
for epoch in range(epochs):
epoch_loss = []
for xx,yy in loader:
means, sigma, w = model(xx)
comp = Normal(means, sigma)
mix = Categorical(w)
gmm = MixtureSameFamily(mix, comp)
likelihood = gmm.log_prob(yy)
loss = -likelihood.mean()
adam.zero_grad()
loss.backward()
adam.step()
epoch_loss.append(loss.item())
losses.append(np.mean(epoch_loss))
However, after a few iterations of decreasing loss, the performance plateaus and the result are deceiving. Specifically, I was expecting the variance to grow with x, but the network is predicting constants means, weights and variance for all x.
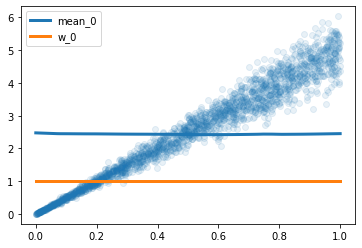
Similar behaviours are observed when I increase the number of gaussians.
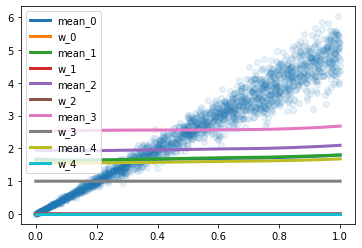
Could someone point me in the right direction ?
Thanks a lot ((: