Hello there,
Please,How can we apply Reinforce or any Policy gradient algorithm when the actions space is multidimensional, let’s say that for each state the action is a vector a= [a_1,a_2,a_3] where a_i are discrete ?
In this case the output of the policy network must model a joint probability distribution
Thanks
You need the reparameterization trick:
if each dimension of your action vector is of the same meaning (same number and meaning of choices), consider about torch.multinomial
if not and each dimension are independent from each other, then create multiple outputs in your network and direct them to multiple categorical distribution, and draw each dimension of your sample from these distributions.
If they are correlated, then you need to build your own model of distribution.
Another option is to map all combinations: a_1 x a_2 x a_3 to a single categorical distribution.
Thanks for your reply ,
Yes, the action vector components are all of the same meaning :
Let’s say that the output of my policy network is a 2D tensor of shape (m,n) (sum of each row equals one)
and I want to generate according to this probability matrix an action vector of size m a = [a_1,…,a_m]
In this case the multinomial distributions is the suitable one ?
yes,you should use the multinomial distribution.
It’s been a while since the question has been asked, yet since I recently faced the same issue I’ll add another answer just for reference and also others’ feedback on its correctness.
(Image from the HuggingFace course)
Following the PG theorem, we need to decompose the joint probability to the product of prob of each action. assuming the actions are independent, we get.
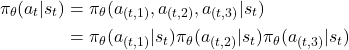
Thus, the log-probs just get added together.
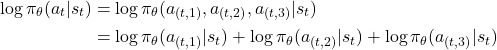
in Pytorch,you’d need to consider 3 separate output heads for the Actor, one for each action (or 3 separate networks, which will be inefficient in learning). It’ll be as
class ActorNet(nn.Module):
def __init__(..., a1_dim, a2_dim, a3_dim, ...):
# ... define arch
self.a1_head = nn.linear(embed_dim, a1_dim)
self.a2_head = nn.linear(embed_dim, a2_dim)
self.a3_head = nn.linear(embed_dim, a3_dim)
def forward(obs):
embed = self.arch(obs)
act1_logits = self.a1_head(embed )
act2_logits = self.a2_head(embed )
act3_logits = self.a3_head(embed )
return act1_logits, act2_logits, act3_logits
actor = ActorNet(..., 5, 4, 8, ...) # would work with different action dims
Then while collecting rollouts:
from torch.distributions import Categorical
def get_action(obs):
act1_logits, act2_logits, act3_logits = actor(obs)
dist_1 = Categorical(logits=act1_logits)
dist_2 = Categorical(logits=act2_logits)
dist_3 = Categorical(logits=act3_logits)
act_1 = dist_1.sample()
act_2 = dist_2.sample()
act_3 = dist_3.sample()
log_prob = dist_1.log_prob(act_1) + dist_2.log_prob(act_2) + dist_3.log_prob(act_3)
return (act_1, act_2, act_3) , log_prob
Now that we have one log_prob and all 3 actions, the rest of the PG algorithm follows the same it normal case.
Note: When estimating the advantage in Actor Critic models, if you use Q as the critic, you will need a1_dim * a2_dim * a3_dim outputs since each action combination is a unique overall action, which gets combinatorically large! Using V would be more efficient.
