Multiple NN with one custom loss function

1

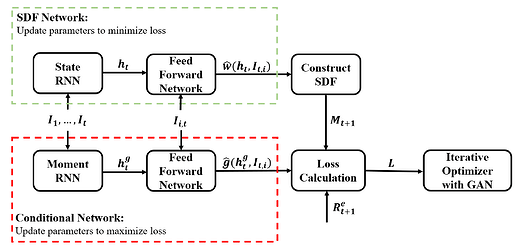
I’m implementing the following architecture:

grafik
grafik1120×539 43.9 KB

with loss:

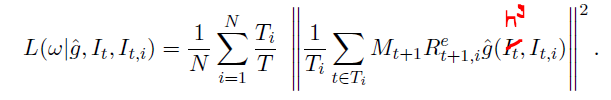
grafik

Both the State and Moment RNN get the same input at time t and feed their hidden states to some Feed Forward Networks along with additional inputs (same for both FFN). Their output then is combined in a custom Loss function.

The whole network is then trained in an iterative way, i.e. 1000 epochs to train the SDF network with given conditional output (minimize loss), then 1000 epochs to train the conditional network given SDF output (minimize negative loss).

I’m not proficient in python (and pytorch), so this may not be best way to implement this:

ap              = AssetPricer(2)                                            # Asset Pricing Neural Network
ad              = Adversary(2)                                              # Adversary Neural Network

srnn            = nn.LSTM(input_size=2, hidden_size=1, num_layers=1, dropout=0.95, batch_first=False)
mrnn            = nn.LSTM(input_size=2, hidden_size=1, num_layers=1, dropout=0.95, batch_first=False)

optimizer_ap    = optim.Adam(ap.parameters(), lr=0.001)                     # APNN optimizer
optimizer_ad    = optim.Adam(ad.parameters(), lr=0.001)                     # ADNN optimizer
optimizer_srnn  = optim.Adam(srnn.parameters(), lr=0.001)
optimizer_mrnn  = optim.Adam(mrnn.parameters(), lr=0.001)                            

train_loss      = []
SR              = []                                                        # Sharpe ratio
N_i             = torch.Tensor(np.count_nonzero(X_train[:,:,1], axis=0))    # Normalization constant

def GMMLoss(M, F, G):
    M       = torch.Tensor(M).unsqueeze(1)
    F       = torch.Tensor(F).unsqueeze(1)
    G       = torch.stack(G)

    R       = X_train[:, :, 1]                          # matrix of t+1 returns, (T X N)
    Z       = (M * R).float()                           # matrix of t+1 returns x M, (T X N)

    Q       = torch.einsum('pnt,tn->pn', G.T, Z)
    Q       = N_i * Q
    Q       = torch.einsum('pn,pn->n', Q, Q)            # squared vector norm
    Loss    = torch.dot((N_i/(N*T)), Q)
    return Loss

# GAN training specs
gan_iter        = [1000, 1000, 1000, 0]                                          
sdf_range       = list(range(len(gan_iter)))[0::2]
adv_range       = list(range(len(gan_iter)))[1::2]

for i in range(len(gan_iterrations)):

    for e in range(gan_iter[i]):

        M = []   # SDF
        F = []   # Tangency portfolio returns
        G = []   # Tensor of moment conditions
        
        for t in train_dates:

            # XSReturns
            rets        = X_train[t,:,1].T

            # State RNN
            inputs_lstm = X_train[0:t+1,:,2:4]
            out_s, _    = srnn(inputs_lstm)
            h_t         = out_s[-1,0,:]*torch.ones(N, 1)

            # Moment RNN
            out_m, _    = mrnn(inputs_lstm)
            h_m         = out_s[-1,0,:]*torch.ones(N, 1)
            
            # Asset Pricer
            x_t         = X_train[t,:,0].unsqueeze(1)
            inputs_ap   = torch.cat((x_t, h_t), 1)
            W           = ap(inputs_ap).flatten()     
            W           = W / W.sum()       

            # Adversary
            inputs_ad   = torch.cat((x_t, h_m), 1)
            g           = ad(inputs_ad)
            G.append(g)
        
            WR          = torch.dot(W, rets)
            M_t1        = 1 - WR
            F.append(WR)
            M.append(M_t1)

        Loss = GMMLoss(M, F, G)
        train_loss.append(Loss)

        if i in sdf_range:
            optimizer_ap.zero_grad()
            optimizer_srnn.zero_grad()
            Loss.backward()
            optimizer_ap.step()
            optimizer_srnn.step()          

        else:       
            optimizer_ad.zero_grad()
            optimizer_mrnn.zero_grad()
            (-Loss).backward()
            optimizer_ad.step()
            optimizer_mrnn.step()

Just to be sure:

  1. As long as the custom loss function contains only torch operations, everything should be fine, correct?
  2. Is my implementation of the iterative training acceptable or does this create problems where I might not see it yet?
        if i in sdf_range:
            optimizer_ap.zero_grad()
            optimizer_srnn.zero_grad()
            Loss.backward()
            optimizer_ap.step()
            optimizer_srnn.step()          

        else:       
            optimizer_ad.zero_grad()
            optimizer_mrnn.zero_grad()
            (-Loss).backward()
            optimizer_ad.step()
            optimizer_mrnn.step()
2
  1. Yes, that is correct. You would get an error, if a method is not differentiable. As a quick test, you could call the backward() method and check all parameters for valid gradients via:
for name, param in model.named_parameters():
    print(name, param.grad)

If any parameter returns a None gradient, you might have accidentally detached the graph at one point.

  1. The condition looks alright and would swap the code paths for each i.
1 Like
3

Thank you very much for taking your time!