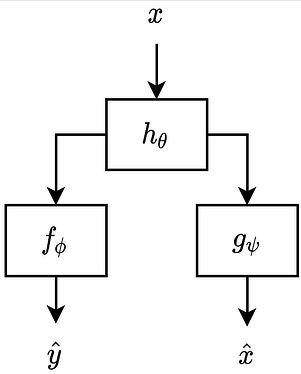
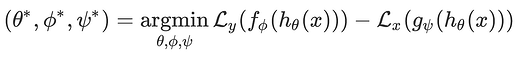Context
I’m currently trying to implement the following architecture:
Where x is an audio signal, h_\theta is a linear filter, f_\phi is a network that predicts one of two classes, either y_hat = 0 or y_hat = 1, and g_\psi is an autoencoder that attempts to reconstruct x as x_\hat.
Here is how I pass a batch of x’s through the filter h_\theta:
x = filt(x)
Where filt is a nn.Module object with trainable parameters:
filt = Filter(bias = True, kernel_size = 201, identity = False).to(device)
After passing x through the filter h_\theta, here is how I pass it through the network f_\phi:
def run_batch_disc(mode,x,labels,transforms,net,loss_func,device):
log, mel, spec = transforms
# compute logarithmic Mel-scale magnitude spectrograms of the filtered
# signals
x = spec(x)
x = torchaudio.functional.complex_norm(x)
x = mel(x)
x = log(x)
# with torch.set_grad_enabled(mode == 'train'):
# logits must have the same shape as labels
logits = net(x).squeeze(dim = 1)
# compute negative log-likelihood (NLL) using logits
NLL = loss_func(logits,labels)
# record predictions. since sigmoid(0) = 0.5, then negative values
# correspond to class 0 and positive values correspond to class 1
preds = logits > 0
# record correct predictions
true_preds = torch.sum(preds == labels)
return NLL,true_preds.item()
Where log, mel, and spec are:
log = torchaudio.transforms.AmplitudeToDB(stype = 'magnitude',
top_db = 80).to(device)
# settings for spectrograms
win_length_sec = 0.012
win_length = int(sample_rate * win_length_sec)
# need 50% overlap to satisfy constant-overlap-add constraint to allow
# for perfect reconstruction using inverse STFT
hop_length = int(sample_rate * win_length_sec / 2) # used to be 64
n_mels = 128
n_fft = 512 # used to be 1024
mel = torchaudio.transforms.MelScale(n_mels = n_mels,
sample_rate = sample_rate,
f_min = 0.0,
f_max = None,
n_stft = n_fft // 2 + 1).to(device)
spec = torchaudio.transforms.Spectrogram(n_fft = n_fft,
win_length = win_length,
hop_length = hop_length,
pad = 0,
window_fn = torch.hann_window,
power = None,
normalized = False,
wkwargs = None).to(device)
In parallel, I am pass the filtered x through the autoencoder g_\psi as follows:
def run_batch_recon(mode,x,spec,net,loss_func,device):
# compute magnitude spectrogram of the filtered signal
x = torchaudio.functional.complex_norm(spec(x))
# scale each magnitude spectrogram in the batch to the interval [0,1]
scale_factor = x.amax(dim=(2,3))[(..., ) + (None, ) * 2]
x_scaled = x / scale_factor
# with torch.set_grad_enabled(mode == 'train'):
# compute reconstruction of the scaled magnitude spectrogram
x_hat = net(x_scaled)
# unscale magnitude spectrogram back to normal values
x_hat = x_hat * scale_factor
# compute reconstruction loss
recon_loss = loss_func(x_hat,x)
return recon_loss
Where loss_func is:
def recon_loss_func(x_hat,x,alpha = 1):
# spectral convergence
num = (x - x_hat).pow(2).sum(dim=(2,3)).sqrt().squeeze()
den = x.pow(2).sum(dim=(2,3)).sqrt().squeeze()
spec_conv = torch.div(num,den)
# log-scale STFT magnitude loss
eps = 1e-10
num = (torch.log(x + eps) - torch.log(x_hat + eps)).abs().sum(dim=2).amax(dim=2).squeeze()
den = torch.log(x + eps).abs().sum(dim=2).amax(dim=2).squeeze()
log_loss = torch.div(num,den)
return torch.mean(spec_conv + alpha * log_loss)
Objective
I am trying to choose the parameters \theta, \phi, and \psi to minimize the following objective function:
Where L_y is the binary cross entropy loss of predicting y_hat not equal to y (NLL in the code above) and L_x is a modified RMSE loss between x and its reconstruction x_hat (recon_loss_func above). Essentially, I am trying to minimize the binary cross entropy loss while maximizing the MSE reconstruction loss. The purpose of this is to choose the filter parameters \theta that balance these two objectives.
Here is how I implement this objective function:
def run_batch(batch,mode,transforms,filt,nets,loss_funcs,lambda_adv,
optimizer,device):
# unpack everything
x,labels = batch
disc_net,recon_net = nets
disc_loss_func, recon_loss_func = loss_funcs
# move to GPU if available
x = x.to(device)
labels = labels.to(device).type_as(x) # needed for NLL
with torch.set_grad_enabled(mode == 'train'):
# filter each signal
x = filt(x)
# compute classification (negative log-likelihood (NLL)) loss and
# number of correct predictions
NLL, true_preds = run_batch_disc(mode,x,labels,transforms,disc_net,
disc_loss_func,device)
# extract speech signals from x and compute reconstruction loss
where_speech = torch.nonzero(labels == 0, as_tuple = True)
recon_loss = run_batch_recon(mode,x[where_speech],transforms[2],
recon_net,recon_loss_func,device)
# compute adversarial loss
adv_loss = NLL - lambda_adv * recon_loss
if mode == 'train':
# compute gradient of adversarial loss with respect to filter,
# discriminator network, and reconstruction network parameters
adv_loss.backward()
# update parameters using the gradient descent update rule
optimizer.step()
# zero the accumulated parameter gradients
optimizer.zero_grad()
return NLL.item(),true_preds,recon_loss.item(),adv_loss.item()
The Problem
As I am trying to implement this, I keep getting all NaN’s in the gradients of the filter parameters \theta once I call .backward() on the objective function shown above, while the gradients of the \phi and \psi of f and g respectively do not contain NaN’s.
I have tried to set
torch.autograd.set_detect_anomaly(True)
And I get the following RuntimeError and traceback:
RuntimeError: Function 'PowBackward0' returned nan values in its 0th output.
C:\ProgramData\Anaconda3\lib\site-packages\torch\autograd\__init__.py:130: UserWarning: Error detected in PowBackward0. Traceback of forward call that caused the error:
File "c:\users\mahmoud talaat\documents\ncsu\semesters\fall2020\ece695_masters_research\adversarial_train_val.py", line 323, in <module>
train_stats = run_epoch('train',
File "c:\users\mahmoud talaat\documents\ncsu\semesters\fall2020\ece695_masters_research\adversarial_train_val.py", line 151, in run_epoch
stats = run_batch(batch,mode,transforms,filt,nets,loss_funcs,
File "c:\users\mahmoud talaat\documents\ncsu\semesters\fall2020\ece695_masters_research\adversarial_train_val.py", line 94, in run_batch
NLL, true_preds = run_batch_disc(mode,x,labels,transforms,disc_net,
File "c:\users\mahmoud talaat\documents\ncsu\semesters\fall2020\ece695_masters_research\adversarial_train_val.py", line 19, in run_batch_disc
x = torchaudio.functional.complex_norm(x)
File "C:\ProgramData\Anaconda3\lib\site-packages\torchaudio\functional.py", line 424, in complex_norm
return complex_tensor.pow(2.).sum(-1).pow(0.5 * power)
(Triggered internally at ..\torch\csrc\autograd\python_anomaly_mode.cpp:104.)
Variable._execution_engine.run_backward(
The part where this RuntimeError happens is here:
def run_batch_disc(mode,x,labels,transforms,net,loss_func,device):
log, mel, spec = transforms
# compute logarithmic Mel-scale magnitude spectrograms of the filtered
# signals
x = spec(x)
x = torchaudio.functional.complex_norm(x)
x = mel(x)
x = log(x)
I have made sure that x = spec(x) is >= 0, but I still get this problem.
I have noticed that if I remove the autoencoder g_\psi, and just pass x through h and f and call backward on the binary cross entropy loss alone, there are no NaN’s in the gradients of the filter parameters.