Hello!
I’ve been working on an implementation of a paper titled “Deep Learning-Based Crack Damage Detection Using Convolutional Neural Networks” by Cha et al. for a couple of days now. In the paper they find some very high accuracy rates, but I have not managed to come even close to those. I’d like some help troubleshooting since I am still pretty new to pytorch.
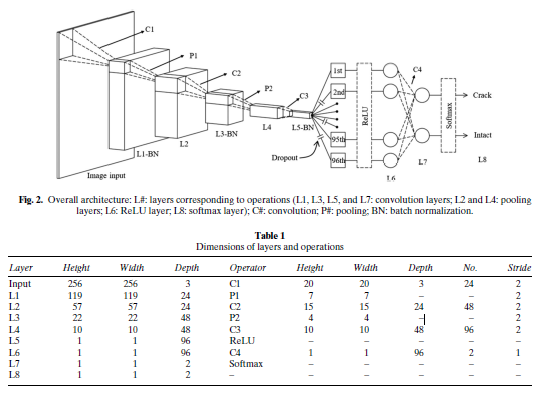
The proposed CNN is described by this diagram and table:
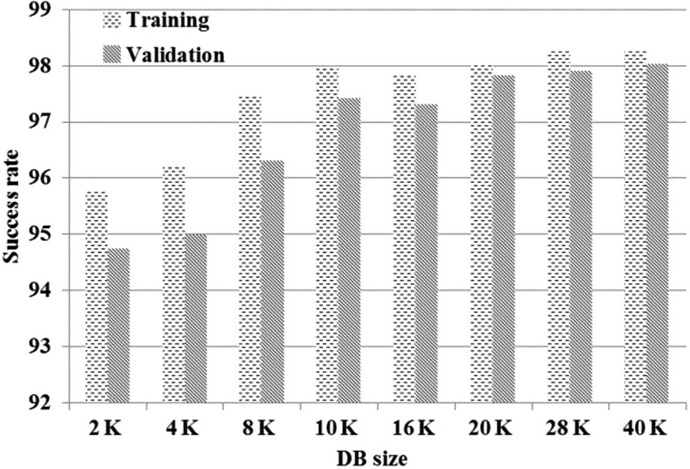
The paper uses a data set of 40.000 images, of which 32.000 training and 8.000 validation. Of these, the ratio between images with cracks and without cracks is 1:1. Images are cropped to 256x256.
Some other given values are:
- Weight decay: 0.0001
- Momentum: 0.9
- Minibatch size: 100 (out of 40K)
- Dropout rate: 0.5
- Learning rate: Starts at 0.01 and logarithmically decreases (I haven’t been able to implement this)
SGD is used for the optimizer.
My network looks like the following:
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.C1 = nn.Conv2d(in_channels=3, out_channels=24, kernel_size=20, stride=2)
self.P1 = nn.MaxPool2d(kernel_size=7, stride=2)
self.C2 = nn.Conv2d(in_channels=24, out_channels=48, kernel_size=15, stride=2)
self.P2 = nn.MaxPool2d(kernel_size=4, stride=2)
self.C3 = nn.Conv2d(in_channels=48, out_channels=96, kernel_size=10, stride=2)
self.C4 = nn.Conv2d(in_channels=96, out_channels=2, kernel_size=1, stride=1)
# The final layer is a softmax layer
self.Softmax = nn.Softmax(dim=1)
self.BN1 = nn.BatchNorm2d(24)
self.BN2 = nn.BatchNorm2d(48)
self.BN3 = nn.BatchNorm2d(96)
self.ReLU = nn.ReLU()
self.Dropout = nn.Dropout2d(0.5)
def forward(self, x):
# Going to take it step by step here to be able to check the values between layers
# This is the order of layers specified in table 1.
x = self.C1(x)
x = self.BN1(x)
x = self.P1(x)
x = self.C2(x)
x = self.BN2(x)
x = self.P2(x)
x = self.C3(x)
x = self.BN3(x)
x = self.Dropout(x)
x = self.ReLU(x)
x = self.C4(x)
x = self.Softmax(x)
return x
And another relevant snippet:
optimizer = optim.SGD(net.parameters(), lr=0.005, momentum=0.9, weight_decay=0.0001)
The results I am getting are around 77% accuracy at the highest versus the paper getting in the high 90s. This accuracy decreases after reaching that highest point, probably due to overfitting.
I also suspect my data set is a bit more varied than the one used in the paper, although the one in the paper is not explicitly shown anywhere. It is also only about 2.300 photos versus the 40.000 of the paper.
Any thoughts on what might be going wrong? Or do I have unrealistic expectations for getting higher accuracies?
Thanks in advance!