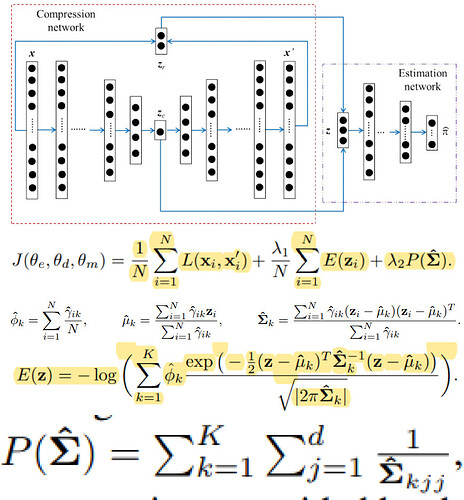
Hey guys! I am picking up Pytorch and at the same time trying to replicate the following model:
My code for the model (modified layer for toy dataset) is:
class DAGMM(nn.Module):
def __init__(self):
super().__init__()
self.encoder = nn.Sequential(
nn.Linear(2, 1),
)
self.decoder = nn.Sequential(
nn.Linear(1, 2),
nn.Tanh()
)
self.en = nn.Sequential(
nn.Linear(2, 3),
nn.Tanh(),
nn.Dropout(),
nn.Linear(3, 4),
nn.Softmax(dim=1)
)
def forward(self, X):
Zc = self.encoder(X)
Xr = self.decoder(Zc)
Re = (X-Xr).norm(dim=1, p=2).view(-1, 1)
Z = torch.cat((Zc.detach(), Re), dim=1)
P = self.en(Z)
return Xr, Z, P
And the loss function:
def loss_fn(X, Xr, Z, P, l1=0.1, l2=0.005):
Phi = P.mean(dim=0)
# Make P (k, n, 1) and Z (1, n, f) to broadcast
Mu = (P.T.unsqueeze(2) * Z.unsqueeze(0)).sum(dim=1) / (P.sum(dim=0).view(-1, 1))
# Same idea, create an extra dimension
cov = (
(
(P.T.unsqueeze(2)) * (Z.unsqueeze(0) - Mu.unsqueeze(1))
).transpose(1, 2) @ (Z.unsqueeze(0) - Mu.unsqueeze(1))
) / (P.sum(dim=0).view(-1, 1).unsqueeze(1))
cov_inv = cov.inverse() #torch.cholesky_inverse(torch.linalg.cholesky(cov))
Zc = Z.unsqueeze(0) - Mu.unsqueeze(1)
E = -(
(
(
(Zc.unsqueeze(2) @ cov_inv.unsqueeze(1)
) @ Zc.unsqueeze(-1)).squeeze(-1).exp()
) * (Phi / (np.pi * cov.det()).sqrt()).view(-1, 1).unsqueeze(1)
).sum(dim=0).log()
P_cov = ((1 / cov.diagonal(dim1=1, dim2=2)).ravel() ** 2).sum().item()
loss = (X-Xr).norm(dim=1, p=2).mean()
loss += l1 * E.mean().item()
loss += l2 * P_cov
return loss
When I run the model, it doesn’t really improve. Given that this is the first time that I am using the framework and making vectorization attempts, I believe that it is probably due to my loss function code.
If you also notice other problems or a best practice that I could adopt, please do tell!