Hi,
I’m trying to use pytorch to define a physics informed neural network (PINN) to solve a problem involving pressure, h and flowrate, q in a pipe as a function of distance, x and time, t.
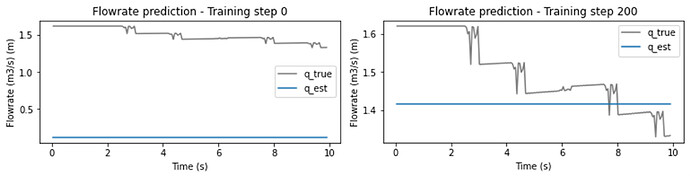
I would like my neural network to output values for h and q at distance = 155m with 160 time steps ranging from 0 - 10 seconds however it outputs the same value across all timesteps as shown in the results below.
As you can see the neural network is learning and the estimated values are moving towards the mean of the true values (shown in grey). But they are moving globally and not one by one which is my issue.
I have used dataset and dataloader to provide inputs to my neural network, these are defined as:
class TrainData(Dataset):
def __init__(self, x_traindata, t_traindata, h_train, q_train):
train_input = torch.cat([x_traindata, t_traindata], axis = 1)
train_aim = torch.cat([h_train, q_train], axis = 1)
self.train_input = train_input
self.train_aim = train_aim
def __len__(self):
return self.train_input.size(0)
def __getitem__(self, idx):
input_value_x = self.train_input[idx, 0]
input_value_t = self.train_input[idx, 1]
output_value_h = self.train_aim[idx, 0]
output_value_q = self.train_aim[idx, 1]
return input_value_x, input_value_t, output_value_h, output_value_q
The architecture is defined as follows, with 2 input nodes, 2 output nodes, 9 hidden nodes and 12 layers.
class FCN(nn.Module):
def __init__(self, N_INPUT, N_OUTPUT, N_HIDDEN, N_LAYERS):
super().__init__()
activation = nn.Tanh
self.fcs = nn.Sequential(
nn.Linear(N_INPUT, N_HIDDEN),
activation()
)
self.fch = nn.Sequential(*[
nn.Sequential(
nn.Linear(N_HIDDEN, N_HIDDEN), # Adjust input size to N_HIDDEN
activation()
) for _ in range(N_LAYERS - 1)
])
self.fce = nn.Linear(N_HIDDEN, N_OUTPUT) # Output layer
def forward(self, x, t):
inputs = torch.cat([x, t], axis = 1)
inputs = self.fcs(inputs)
inputs = self.fch(inputs)
outputs = self.fce(inputs)
return outputs
pinn = FCN(2, 2, 9, 12)
As part of the PINN pytorch analyses differential equations at multiple different time and distance points (collocation points) to ensure that the differential equations equal 0 at all these points to ensure the physical laws are obeyed. This is defined as shown below
class CollocData(Dataset):
def __init__(self, x_colloc, t_colloc):
colloc_input = torch.cat([x_colloc, t_colloc], axis = 1)
self.colloc_input = colloc_input
def __len__(self):
return self.colloc_input.size(0)
def __getitem__(self, idx):
input_x = self.colloc_input[idx, 0]
input_t = self.colloc_input[idx, 1]
return input_x, input_t
x_colloc = torch.linspace(0, 200, 500).view(-1,1).requires_grad_(True)
t_colloc = torch.linspace(0, 10, 500).view(-1,1).requires_grad_(True)
The dataloaders are then defined using:
test_dataset = TrainData(x_train, t_train, h_train, q_train)
colloc_dataset = CollocData(x_colloc, t_colloc)
train_dataloader = DataLoader(test_dataset, batch_size = x_train.size(0), shuffle=True)
colloc_dataloader = DataLoader(colloc_dataset, batch_size = x_colloc.size(0), shuffle = True)
The main training loop for the Neural Network has been coded as follows:
optimiser = torch.optim.SGD(pinn.parameters(), lr = 1e-3)
start_time = time.time()
for i in range (200001):
for train_batch, colloc_batch in zip(train_dataloader, colloc_dataloader):
optimiser.zero_grad()
train_x, train_t, target_h, target_q = train_batch
colloc_x, colloc_t = colloc_batch
colloc_output = pinn(colloc_x.unsqueeze(1), colloc_t.unsqueeze(1))
h_hat, q_hat = colloc_output[:,0], colloc_output[:,1]
dq_dt = torch.autograd.grad(q_hat, t_colloc, torch.ones_like(q_hat), create_graph=True)[0]
dq_dx = torch.autograd.grad(q_hat, x_colloc, torch.ones_like(q_hat), create_graph=True)[0]
dh_dt = torch.autograd.grad(h_hat, t_colloc, torch.ones_like(h_hat), create_graph=True)[0]
dh_dx = torch.autograd.grad(h_hat, x_colloc, torch.ones_like(h_hat), create_graph=True)[0]
F1 = (Cs_A * dq_dt) + (q_hat * dq_dx) + (g * Cs_A**2 * dh_dx) + (f * ((torch.abs(q_hat) * q_hat) / (2 * diam)))
F2 = (Cs_A * dh_dt) + (q_hat * dh_dx) + ((a**2/g) * dq_dx)
loss_pde = torch.mean(F1**2 + F2**2)
train_output = pinn(train_x.unsqueeze(1), train_t.unsqueeze(1))
hq_true = torch.cat([h_train, q_train], axis = 1)
loss_data = torch.mean((train_output - hq_true)**2)
loss = w_f * loss_pde + loss_data
loss.backward()
optimiser.step()
I hope this is clear and you understand what the problem is if not please leave a comment and I can explain further thanks.