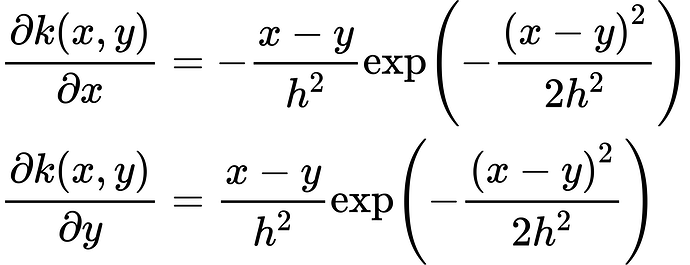No difference in gradient of Gaussian Kernel derivative (Cross Covariance matrix) wrt inputs

autograd
1

Hello, I’m trying to understand why the gradient returned by autograd does not change w.r.t. the input in a Gaussian kernel. More specifically, suppose we have the following naive implementation of the RBF kernel:

def naive_rbf(X, Y, h):
    batch, _ = X.shape
    Kxy = torch.empty(batch, batch)
    dx_Kxy = torch.zeros_like(X)
    dy_Kxy = torch.zeros_like(X)
    for i in range(batch):
        for j in range(batch):
            # using row vectors
            diff = X[i] - Y[j]
            norm = diff @ diff.T
            Kxy[i, j] = (-0.5 / h ** 2 * norm).exp()
            dx_Kxy[i] += -diff * Kxy[i, j] / h ** 2
            dy_Kxy[j] += diff * Kxy[i, j] / h ** 2
    return Kxy, dx_Kxy, dy_Kxy

So, given that:

image
image1853×712 55.9 KB

I’d expect the gradients w.r.t. different inputs to have opposite signs.

However, if I run:

BATCH, DIM = [20, 5]
X = torch.randn(BATCH, DIM)
h = torch.tensor(1.0)

Xg = X.clone().requires_grad_()
K = naive(Xg, X, h)[0]
dx_K = grad(K.sum(), Xg, h)[0]

Xg = X.clone().requires_grad_()
K = naive(X, Xg, h)[0]
dy_K = grad(K.sum(), Xg, h)[0]
torch.allclose(dx_K, dy_K)  # True

Can anyone shed some light on why this happens?