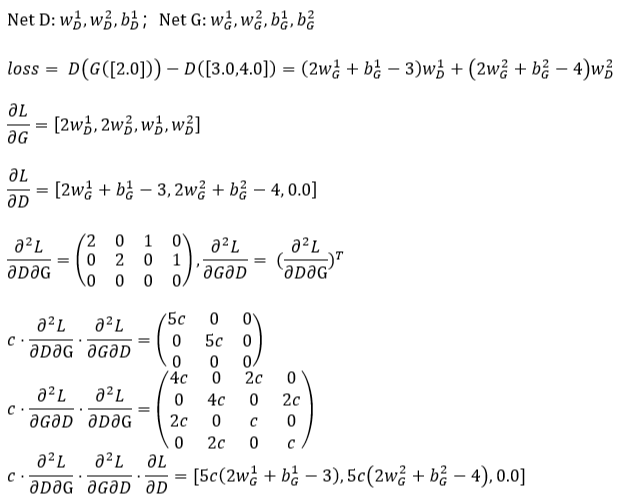Hi, I found a problem that seems to be a numerical issue related to Hessian vector product. In the following code, I compare the difference between the result that obtained by Hessian vector product and the true value obtained by handcrafted derivatives. Pytorch 1.4.0, CPU
import torch
import torch.nn as nn
import torch.autograd as autograd
def Hvp_vec(grad_vec, params, vec, retain_graph=False):
'''
return Hessian vector product
'''
grad_grad = autograd.grad(grad_vec, params, grad_outputs=vec, retain_graph=retain_graph,
allow_unused=True)
grad_list = []
for i, p in enumerate(params):
if grad_grad[i] is None:
grad_list.append(torch.zeros_like(p))
else:
grad_list.append(grad_grad[i].contiguous().view(-1))
hvp = torch.cat(grad_list)
return hvp
class NetD(nn.Module):
def __init__(self):
super(NetD, self).__init__()
self.net = nn.Linear(2, 1)
self.weight_init()
def forward(self, x):
return self.net(x)
def weight_init(self):
self.net.weight.data = torch.Tensor([[1.0, 2.0]])
self.net.bias.data = torch.Tensor([-1.0])
class NetG(nn.Module):
def __init__(self):
super(NetG, self).__init__()
self.net = nn.Linear(1, 2)
self.weight_init()
def forward(self, x):
return self.net(x)
def weight_init(self):
self.net.weight.data = torch.Tensor([[3.0], [-1.0]])
self.net.bias.data = torch.Tensor([-4.0, 3.0])
lr = 0.01
factor = lr
D = NetD()
G = NetG()
z = torch.tensor([2.0])
real_x = torch.tensor([[3.0, 4.0]])
loss = D(G(z)) - D(real_x)
d_param = list(D.parameters())
g_param = list(G.parameters())
grad_g = autograd.grad(loss, g_param, create_graph=True, retain_graph=True)
grad_g_vec = torch.cat([g.contiguous().view(-1) for g in grad_g])
grad_d = autograd.grad(loss, d_param, create_graph=True, retain_graph=True)
grad_d_vec = torch.cat([g.contiguous().view(-1) for g in grad_d])
g_vec_d = grad_g_vec.clone().detach()
d_vec_d = grad_d_vec.clone().detach()
A_g = torch.tensor([[4.0 * factor, 0.0, 2.0 * factor, 0],
[0.0, 4.0 * factor, 0.0, 2.0 * factor],
[2.0 * factor, 0.0, factor, 0.0],
[0.0, 2.0 * factor, 0.0, factor]])
A_d = torch.tensor([[5.0 * factor, 0.0, 0.0],
[0.0, 5.0 * factor, 0.0],
[0.0, 0.0, 0.0]])
g_test = g_vec_d
d_test = d_vec_d
g_gt = g_vec_d.clone()
d_gt = d_vec_d.clone()
d_diffs = []
g_diffs = []
for i in range(1):
g_gt = torch.matmul(A_g, g_gt)
d_gt = torch.matmul(A_d, d_gt)
tmp1 = Hvp_vec(grad_d_vec, g_param, d_test, retain_graph=True).detach()
d_test = Hvp_vec(grad_g_vec, d_param, tmp1, retain_graph=True).detach().mul(factor)
tmp2 = Hvp_vec(grad_g_vec, d_param, g_test, retain_graph=True).detach()
g_test = Hvp_vec(grad_d_vec, g_param, tmp2, retain_graph=True).detach().mul(factor)
g_diffs.append((g_gt - g_test).tolist())
d_diffs.append((d_gt - d_test).tolist())
print('%.3f * D_dg * D_gd * grad_d :' % factor)
print(d_diffs)
print('%.3f * D_gd * D_dg * grad_g :' % factor)
print(g_diffs)
The following figure explains the situation where the issue occurs. I build a toy GAN model here, which includes discriminator D and generator G. I try to compute this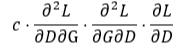 
. When the factor (c) is bigger than 0.1, it’s consistent with the true value. But if the factor is 0.04, 0.01, there’s some difference between the result and true value.
c= 0.05
0.050 * D_dg * D_gd * grad_d :
[[0.0, 0.0, 0.0]]
0.050 * D_gd * D_dg * grad_g :
[[0.0, 0.0, 0.0, 0.0]]
c= 0.04
0.040 * D_dg * D_gd * grad_d :
[[-1.4901161193847656e-08, -5.960464477539063e-08, 0.0]]
0.040 * D_gd * D_dg * grad_g :
[[0.0, 0.0, 0.0, 0.0]]
c=0.01
0.010 * D_dg * D_gd * grad_d :
[[-3.725290298461914e-09, -1.4901161193847656e-08, 0.0]]
0.010 * D_gd * D_dg * grad_g :
[[0.0, 0.0, 0.0, 0.0]]
