Hi everyone,
I want to optimize a NN using Varitional-Optimization instead of pure backprob.
Consider following set:
-
We have a NN with weights → f(w)
-
We have some samples ‘z_i’ from a normal-dist. → z_i ∼ N(0, 1)
Now for applying VO on our NN, we have following equations:
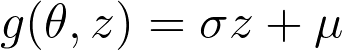
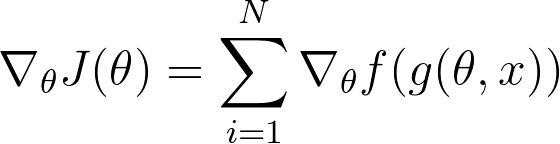
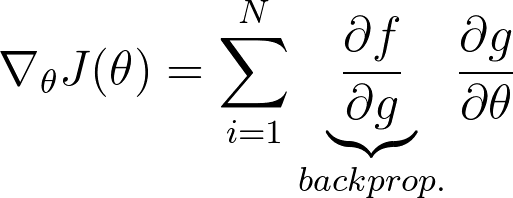
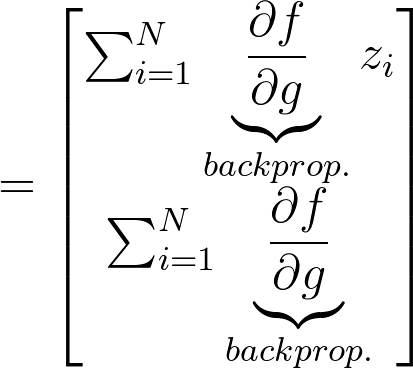
My problem is now how can i moultiply the gradient w.r.t. to the weights of the function g(theta, z) with the grads of the netowrk?
i saw that i can pass a “grad”-variabel to the backward-fucntion but what should be the shape of the variable for applying it to all weights of the network?
this my code right now:
class VOFast(optim.Optimizer):
def __init__(self, params, sample_size=100, mu=0.0, log_sigma=-4.0, interoptim=optim.Adam, alpha=0.9, **kwargs):
defaults = dict(sample_size=sample_size)
params = list(params)
mean = []
logsigma = []
for param in params:
len = self.param_length(param)
mean_ = torch.Tensor(len)
logsigma_ = torch.Tensor(len).fill_(log_sigma)
if cuda_enabled:
mean_ = mean_.cuda()
logsigma_ = logsigma_.cuda()
mean_ = Variable(mean_, requires_grad=True)
mean_.data[...] = param.data[...]
logsigma_ = Variable(logsigma_, requires_grad=True)
mean.append(mean_)
logsigma.append(logsigma_)
self.optimizer_ = interoptim([{"params": mean}, {"params": logsigma}], **kwargs)
param_groups = [dict(params=params, name="params"),
dict(params=mean, name="mean"),
dict(params=logsigma, name="logsigma")]
super(VOFast, self).__init__(param_groups, defaults)
self.baseline = None
self.baselines = []
self.alpha = alpha
def __setstate__(self, state):
super(VOFast, self).__setstate__(state)
def zero_grad(self):
self.optimizer_.zero_grad()
def step(self, closure):
sample_size = self.param_groups[0]['sample_size']
params = self.param_groups[0]["params"]
mean = self.param_groups[1]["params"]
logsigma = self.param_groups[2]["params"]
for i in range(sample_size):
for idx, mu in enumerate(mean):
samples = Variable(torch.randn(len(mu)), requires_grad=False)
if cuda_enabled:
samples = samples.cuda()
samples = samples.detach()
z = torch.exp(logsigma[idx]) * samples + mean[idx]
if cuda_enabled:
z = z.cuda()
params[idx].data[...] = z.view(params[idx].shape).data
loss_closure = closure()
# here we shoudl actualy pass the grads w.r.t. to mean ans sigma to the backward-func!
loss_closure.backward()
self.optimizer_.step()
def voptim(net, loss_func, trainloader, mean_val=1.0,
log_sigma=-1.0, sample_size=100, lr=0.1, threshold=0.9):
"""
vanilla natrual evolution strategy
:param net:
:param loss_func:
:param lr:
:return:
"""
kwargs = dict(lr=lr) # adam
# kwargs = dict(lr=lr, momentum=0.9) # sgd
optimizer = VOFast(net.parameters(), sample_size=sample_size, interoptim=optim.Adam,
log_sigma=log_sigma, mu=mean_val, alpha=0.9, **kwargs)
for epoch in range(2):
for i, data in enumerate(trainloader, 0):
X_tr, y_tr = data
if cuda_enabled:
X_tr = X_tr.cuda()
y_tr = y_tr.cuda()
X_train = Variable(X_tr)
y_train = Variable(y_tr)
def closure(input=X_train, target=y_train):
output = net(input)
loss = loss_func(output, target)
return loss
optimizer.zero_grad()
optimizer.step(closure=closure)
if i % 10 == 0:
out = net(X_train)
loss = loss_func(out, y_train)
_, predicted = torch.max(out.data, 1)
accuracy = 100 * torch.sum(y_train.data == predicted) / y_train.data.size()[0]
print('[%d.%d], loss = %.2f, accuracy %d %%' % (epoch, i, loss.data[0], np.ceil(accuracy)))
return
thanks