Permute on tensor whose ndim > 2

1

Hello,

I am always confused about the permute operation on tensors whose dim are greater than 2.
When in 2D dimension, the permute operation is easy to understand, it is just a transpose of a matrix.
But when it comes to higher dimension, I find it really hard to think.
Personally, I will consider 2D tensor as matrix, 3D tensor as a list of matrix, 4D tensor as a list of cubic.

In practice, I know that permute operation is used to change the dimension. For example in NLP, we can use example_tensor.permute(1,0,2) to change from (batch_size,seq_len,hid_dim) to (seq_len,batch_size,hid_dim). But how does this happen? Why the float number in a tensor just miraculously become the shape we want it to be?

Is there any mental model to figure this out? Thanks very much !

Actually this confusion comes from this code snippet:

import torch
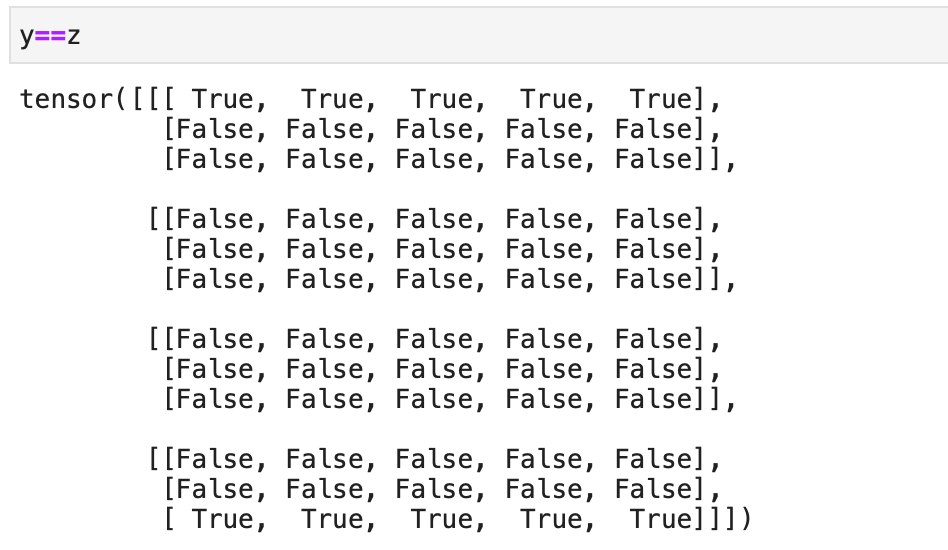
x = torch.arange(3*4*5).reshape(3,4,5)
y = x.reshape(4,3,5)
z = x.permute(1,0,2)

And it turns out that y is not equal to z.

image
image948×550 13.6 KB

I know maybe I can take 3D as a list of matrix to figure out why y is not equal to z. But I want to know if there is more general way to this kind of problem. Or how do you guys think about high dimensional tensor?

1 Like
2

In your example, memory is shared by three views, and 0…60 sequence is never reordered in memory, you’re just assigning different indexes to same memory cells. Tensor.stride() may may helpful to understand permuted tensors:

x.stide() -> 20,5,1
y.stride() -> 15,5,1
z.stride() -> 5, 20,1
multiplying these values by indexes gives you a memory offset used to access data
so y[1,0,0] = 15 (value 15 at offset 15), but z[1,0,0] = 5

3

But How can we calculate z.stride() manually? thanks!

4

It is permuted x.stride(), i.e. you just select dimensions in a different order.
Initial (contiguous tensor) values for A,B,C,D sized tensor are B*C*D,C*D,D,1