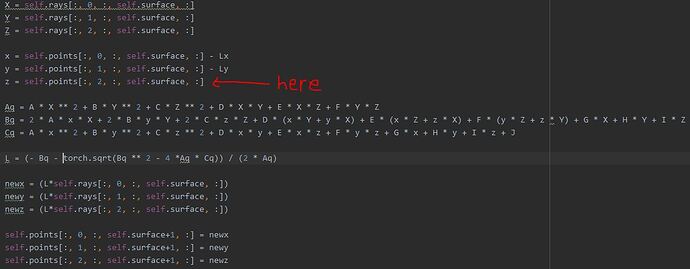
I keep getting the error one of the variables needed for gradient computation has been modified by an in-place operation but I don’t think I have made any in place operations. Below is the code that is causing the error, it specifically points to the line with Cq, and I can reproduce the error by just setting Cq = xz (lowercase x and z), but it runs fine with Cq = xy. Points and rays are tensors with xyz values as the second dimension which have been initialized with zeros. ABCD etc…have been initialized externally and don’t use the points or rays for computation, so shouldn’t cause any issues. When I subtract zero in the location shown in the picture, the problem seems to go away but I am having similar problems in other places in the code and want to know what is actually going on.
Image of code below or attached, I’m not really sure how it works. Also any tips for speed improvement are welcome.
- The in-place operation could possibly be on
self.pointsas it was referenced and used then modified . I’m not exactly sure if this is the case. - Subtracting the zero solves the problem by creating a copy of the selected indexes; in this case subtracting the zero would be equivalence to
self.points[SOMETHING].clone()
yes I believe it is on self.points, but I don’t understand why. I grab points from one part of the tensors (at slice self.surface which is an integer=0 in this example) modify them with lots of intermediate outputs and then put them in self.points[:, :, :, self.surface+1, :]. I get that I can stop the problem with a clone, but I’m trying to understand why there is a problem in the first place.
Let’s say the indexes u grabed from self.points is II. First, u did x=self.points[II], so every operation on x will track a history back to self.points[II]. But in the end u modified self.points[II], which is part of the earlier graph. My understandings may not be totally correct,