Hey all,
I’ve been trying to construct a PINN to solve the 1D heat equation. My code is as follows:
def train_model(architecture, epochs, learning_rate, model_name, pinn=True):
# architecture :- (PI)NN object
# epochs :- int indicating num epochs
# learning_rate :- float indicating learning learning_rate
# model_name :- string indicating model name
# pinn :- bool indicating if the object is meant to be a PINN
model = architecture
model.to(device)
model.train()
optimiser = optim.Adam(model.parameters(), lr=learning_rate)
# optimiser = optim.LBFGS(model.parameters(), lr=learning_rate)
# Total loss
losses_physics = []
# Data loss in case of known solution
data_losses = []
# Physics losses
diff_eqn_losses = []
lb_losses = []
ub_losses = []
ic_losses = []
lambda_eqn, lambda_ub, lambda_lb, lambda_ic = 0.7, 0.1, 0.1, 0.1
for i in range(epochs):
optimiser.zero_grad()
loss_function = nn.MSELoss()
x, t, k = get_random_data()
x_c, x_ub, x_lb, x_i, t_c, t_ub, t_lb, t_i, k_c, k_ub, k_lb, k_i = split_data(x, t, k)
equation_target = torch.zeros_like(x_c)
# Default boundary conditions
upper_boundary = 0
lower_boundary = 0
ub_target = (torch.ones_like(x_ub) * upper_boundary).to(device)
lb_target = (torch.ones_like(x_lb) * lower_boundary).to(device)
ic_target = (u_heat(x_i, t_i, k_i)).to(device)
x_c.requires_grad_(True)
t_c.requires_grad_(True)
k_c.requires_grad_(True)
if pinn:
u_pred_eqn = model(x_c, t_c, k_c)
du_dt = torch.autograd.grad(u_pred_eqn, t_c, torch.ones_like(t_c), create_graph=True)[0]
du_dx = torch.autograd.grad(u_pred_eqn, x_c, torch.ones_like(x_c), create_graph=True)[0]
d2u_dx2 = torch.autograd.grad(du_dx, x_c, torch.ones_like(x_c), create_graph=True)[0]
equation = du_dt - (k_c * d2u_dx2)
physics_loss = lambda_eqn * (1/x_c.numel()) * loss_function(equation, equation_target)
upper_boundary_pred = model(x_ub, t_ub, k_ub)
lower_boundary_pred = model(x_lb, t_lb, k_lb)
initial_condition_pred = model(x_i, t_i, k_i)
ub_loss = lambda_ub * (1/x_ub.numel()) * loss_function(upper_boundary_pred, ub_target)
lb_loss = lambda_lb * (1/x_lb.numel()) * loss_function(lower_boundary_pred, lb_target)
ic_loss = lambda_ic * (1/x_i.numel()) * loss_function(initial_condition_pred, ic_target)
loss = physics_loss + ic_loss + ub_loss + lb_loss
# Total loss
losses_physics.append(loss.item())
# Physics lossses
diff_eqn_losses.append(physics_loss.item())
lb_losses.append(lb_loss.item())
ub_losses.append(ub_loss.item())
ic_losses.append(ic_loss.item())
else:
u_target = (u_heat(x, t, k)).to(device)
u_pred = model(x, t, k)
data_loss = loss_function(u_pred, u_target)
loss = (1/x.numel()) * data_loss
# Total loss
data_losses.append(loss.item())
if (i+1) % 1000 == 0:
print(f"{i+1}/{epochs} : {loss}")
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), 1)
optimiser.step()
if pinn:
loss_dictionary = {
"total_loss": losses_physics,
"physics_loss": diff_eqn_losses,
"lb_loss": lb_losses,
"ub_loss": ub_losses,
"ic_loss": ic_losses
}
else:
loss_dictionary = {
"total_loss": data_losses
}
write_data_folder(model_name, loss_dictionary)
torch.save(model.state_dict(), f"final_models/{model_name}.pt")
For each epoch, I sample a total of 4000 points within a domain of x, t and k. I then split them into their various datasets: collocation points (x_c, t_c, k_c), boundary points (x_ub/x_lb, t_ub…) and initial points (x_i, t_i, k_i). I then compute the residuals and use the MSE loss function to compute the loss. I get a low loss of around 7.78e-08. But when testing, it produces really bad results.
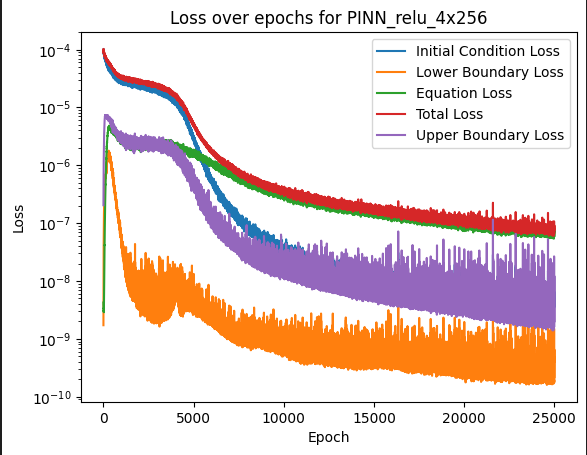
My network takes 3 inputs and has 1 output. I have 4 hidden layers of 256 nodes and I used the relu activation function. Looking at the losses, it appears that the residual from the equation contributes the most, and so I gave it a higher weight (in the total loss calculation) so that the network focuses on it more.
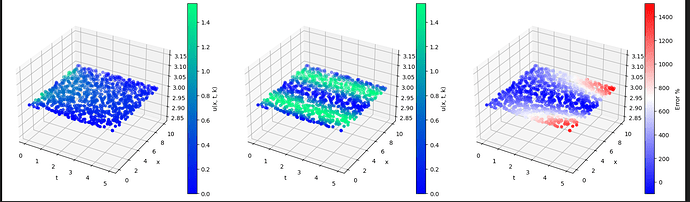
Despite the low loss, it performs absolutely horrendously:
Here the first pic is the expected, the second is the prediction and the third is the error. What’s more is that these graphs make absolutely no sense?? This is how I compute the error:
test_data_size = 1000
x_min_test, x_max_test, t_min_test, t_max_test, k_min_test, k_max_test = 0, 10, 0, 5, 2, 4
x_test = (torch.rand(test_data_size) * (x_max_test - x_min_test) + x_min_test).view(-1, 1).to(device)
t_test = (torch.rand(test_data_size) * (t_max_test - t_min_test) + t_min_test).view(-1, 1).to(device)
# k_test = (torch.rand(test_data_size) * (k_max_test - k_min_test) + k_min_test).view(-1, 1).to(device)
k_test = (torch.ones_like(x_test) * 3).to(device)
correct_u = u_heat(x_test, t_test, k_test)
# print(correct_u)
model = model.to(device)
model.load_state_dict(torch.load(f"final_models/{model_name}.pt"))
model.eval()
predicted_u = model(x_test, t_test, k_test)
# print(predicted_u)
error = ((- correct_u + predicted_u) / (correct_u)) * 100
# print(error)
fig = plt.figure(figsize=(20, 50))
ax1 = fig.add_subplot(131, projection='3d')
x = x_test.cpu().detach().numpy()
t = t_test.cpu().detach().numpy()
k = k_test.cpu().detach().numpy()
u = correct_u.cpu().detach().numpy()
vmin = min(torch.min(correct_u), torch.min(predicted_u))
vmax = max(torch.max(correct_u), torch.max(predicted_u))
img = ax1.scatter(t, x, k, c=u, cmap=plt.winter())
ax1.set_xlabel("t")
ax1.set_ylabel("x")
ax1.set_zlabel("k", labelpad=1)
img.set_clim(vmin, vmax)
cbar = fig.colorbar(img, fraction = 0.05)
cbar.set_label("u(x, t, k)")
u_p = predicted_u.cpu().detach().numpy()
ax2 = fig.add_subplot(132, projection='3d')
img = ax2.scatter(t, x, k, c=u_p, cmap=plt.winter())
ax2.set_xlabel("t")
ax2.set_ylabel("x")
ax2.set_zlabel("k", labelpad=1)
img.set_clim(vmin, vmax)
cbar = fig.colorbar(img, fraction = 0.05)
cbar.set_label("u(x, t, k)")
e = error.cpu().detach().numpy()
ax3 = fig.add_subplot(133, projection='3d')
img = ax3.scatter(t, x, k, c=e, cmap=plt.get_cmap("bwr"))
ax3.set_xlabel("t")
ax3.set_ylabel("x")
ax3.set_zlabel("k", labelpad=1)
cbar = fig.colorbar(img, fraction = 0.05)
cbar.set_label("Error %")
plt.show()
Can someone help me make sense of what is happening? And possibly improve/correct any mistakes. Here is how I create the datasets:
training_inputs = 3
# You have 4 kinds of data: collocation points, 2 sets of data on the boundaries and 1 set of data for the initial condition
training_data_types = 4
# How much training data per type of data
data_type_size = 1000
training_data_size = data_type_size * training_data_types
def get_random_data():
# Collocation points #######################################
x_collocation = torch.rand(data_type_size) * (x_max - x_min) + x_min
t_collocation = torch.rand(data_type_size) * (t_max - t_min) + t_min
x_collocation = x_collocation.view(-1, 1).to(device)
t_collocation = t_collocation.view(-1, 1).to(device)
# Upper boundary ###########################################
x_upper_boundary = torch.ones_like(x_collocation) * x_max
t_upper_boundary = torch.rand(data_type_size) * (t_max - t_min) + t_min
x_upper_boundary = x_upper_boundary.view(-1, 1).to(device)
t_upper_boundary = t_upper_boundary.view(-1, 1).to(device)
# Lower boundary ###########################################
x_lower_boundary = torch.ones_like(x_collocation) * x_min
t_lower_boundary = torch.rand(data_type_size) * (t_max - t_min) + t_min
x_lower_boundary = x_lower_boundary.view(-1, 1).to(device)
t_lower_boundary = t_lower_boundary.view(-1, 1).to(device)
# Initial data ##############################################
x_initial = torch.rand(data_type_size) * (x_max - x_min) + x_min
t_initial = torch.ones_like(t_collocation) * t_min
x_initial = x_initial.view(-1, 1).to(device)
t_initial = t_initial.view(-1, 1).to(device)
x_train = torch.cat((x_collocation, x_upper_boundary, x_lower_boundary, x_initial), dim=0)
t_train = torch.cat((t_collocation, t_upper_boundary, t_lower_boundary, t_initial), dim=0)
k_train = (torch.rand(x_train.numel()) * (k_max - k_min) + k_min).view(-1, 1).to(device)
return x_train, t_train, k_train
def split_data(x_data, t_data, k_data):
x_train_collocation = x_data[: data_type_size * 1]
x_train_upper = x_data[data_type_size * 1 : data_type_size * 2]
x_train_lower = x_data[data_type_size * 2 : data_type_size * 3]
x_train_initial = x_data[data_type_size * 3 : ]
t_train_collocation = t_data[: data_type_size * 1]
t_train_upper = t_data[data_type_size * 1 : data_type_size * 2]
t_train_lower = t_data[data_type_size * 2 : data_type_size * 3]
t_train_initial = t_data[data_type_size * 3 : ]
k_train_collocation = k_data[: data_type_size * 1]
k_train_upper = k_data[data_type_size * 1 : data_type_size * 2]
k_train_lower = k_data[data_type_size * 2 : data_type_size * 3]
k_train_initial = k_data[data_type_size * 3 : ]
return x_train_collocation, x_train_upper, x_train_lower, x_train_initial, \
t_train_collocation, t_train_upper, t_train_lower, t_train_initial, \
k_train_collocation, k_train_upper, k_train_lower, k_train_initial
# print(k_train)
# print(k_train_upper)
# print(k_train_lower)
# print(k_train_initial)
x, t, k = get_random_data()
x_c, x_ub, x_lb, x_i, t_c, t_ub, t_lb, t_i, k_c, k_ub, k_lb, k_i = split_data(x, t, k)
print(x.shape, t.shape, k.shape)