Post Training Static Quantization API still uses float weights instead of int?

[ashmallow (Asher Mai)]

I find that floating point values are still being stored and used during inference in a quantized model

I understand that quantization is to convert model weights from floating point to integer weights (specifically float32 to quint8). When I print out the quantized inputs, outputs, and weights of an example given on the Pytorch Quantization documentation, you can see in the picture that they are stored as float32 numbers with scale and zero_point. I understand that the integer representation ( .int_repr() ) of these quantized tensors are calculated by dividing these float32 numbers by scale and adding zero_point, and then rounding. However, in my experimenting, I find that these integer representations of the tensors are not being used during inferencing. The float32 parts of the quantized input, weights and outputs are the only parts being used during inferencing without using these zero_point and scale associated with each tensor.

So my question is, what is the meaning of quantization if floating point values are still involved with the inferencing process, and how does that reduce the memory by a quarter of the original size if these floating point values still need to be stored in memory?

Thank you in advance. Any input would be hugely appreciated.

[ddang (David)]

the integer values are used for computations (e.g., when convolving or during matmul). the values you’re printing are the dequantized values. to print the integer values, you need to call int_repr()

[ashmallow (Asher Mai)]

Hi David, Thank you for the reply. Yes I understand I can get the integer values using int_repr(). However, when I try to replicate the results produced by forward() manually, I find that int_repr() are not used for computation, because that would cause the output numbers to be in the 100,000s, which is way out of range of 8 bits. I find that if I use the dequantized float numbers to manually do the convolution / linear matrix multiplications, then I would create the same results produced by the forward().

As you can see in the image below, the first output is produced by me using the dequantized floating point values. (for the convolution I just did a simple multiply because it’s a 1x1 kernel with 1 channel).
And the second cell outputs the results produced by the forward() when you run model_int8(input). You can see that they pretty much match up with each other, meaning that the forward() function also uses the floating point numbers for computation instead of the int_repr().

For reference, the model and quantization method I used is from the example given by the Pytorch quantization documentation: Quantization — PyTorch 2.1 documentation.

import torch

class M(torch.nn.Module):
    def __init__(self):
        super(M, self).__init__()
        # QuantStub converts tensors from floating point to quantized
        self.quant = torch.quantization.QuantStub()
        self.conv = torch.nn.Conv2d(1, 1, 1)
        self.relu = torch.nn.ReLU()
        # DeQuantStub converts tensors from quantized to floating point
        self.dequant = torch.quantization.DeQuantStub()

    def forward(self, x):
        # manually specify where tensors will be converted from floating
        # point to quantized in the quantized model
        x = self.quant(x)
        x = self.conv(x)
        x = self.relu(x)
        # manually specify where tensors will be converted from quantized
        # to floating point in the quantized model
        x = self.dequant(x)
        return x

# create a model instance
model_fp32 = M()

# model must be set to eval mode for static quantization logic to work
model_fp32.eval()

model_fp32.qconfig = torch.quantization.get_default_qconfig('fbgemm')

model_fp32_fused = torch.quantization.fuse_modules(model_fp32, [['conv', 'relu']])

model_fp32_prepared = torch.quantization.prepare(model_fp32_fused)

input_fp32 = torch.randn(4, 1, 4, 4)
model_fp32_prepared(input_fp32)

model_int8 = torch.quantization.convert(model_fp32_prepared)

res = model_int8(input_fp32)

Hope this all makes sense. And thanks for taking the time to answer my question.

[ashmallow (Asher Mai)]

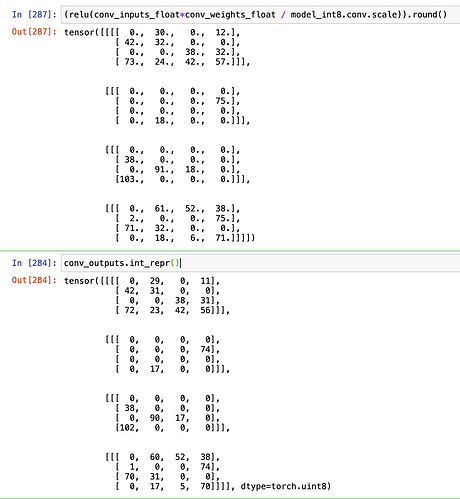
I’ve attached the code and output I used to find out that they actually use the dequantized float values for computation during forward pass.

import torch

# define a floating point model where some layers could be statically quantized
class M(torch.nn.Module):
    def __init__(self):
        super(M, self).__init__()
        # QuantStub converts tensors from floating point to quantized
        self.quant = torch.quantization.QuantStub()
        self.conv = torch.nn.Conv2d(1, 1, 1)
        self.relu = torch.nn.ReLU()
        # DeQuantStub converts tensors from quantized to floating point
        self.dequant = torch.quantization.DeQuantStub()

    def forward(self, x):
        # manually specify where tensors will be converted from floating
        # point to quantized in the quantized model
        x = self.quant(x)
        x = self.conv(x)
        x = self.relu(x)
        # manually specify where tensors will be converted from quantized
        # to floating point in the quantized model
        x = self.dequant(x)
        return x

# create a model instance
model_fp32 = M()

# model must be set to eval mode for static quantization logic to work
model_fp32.eval()

# attach a global qconfig, which contains information about what kind
# of observers to attach. Use 'fbgemm' for server inference and
# 'qnnpack' for mobile inference. Other quantization configurations such
# as selecting symmetric or assymetric quantization and MinMax or L2Norm
# calibration techniques can be specified here.
model_fp32.qconfig = torch.quantization.get_default_qconfig('fbgemm')


# Fuse the activations to preceding layers, where applicable.
# This needs to be done manually depending on the model architecture.
# Common fusions include `conv + relu` and `conv + batchnorm + relu`
model_fp32_fused = torch.quantization.fuse_modules(model_fp32, [['conv', 'relu']])

# Prepare the model for static quantization. This inserts observers in
# the model that will observe activation tensors during calibration.
model_fp32_prepared = torch.quantization.prepare(model_fp32_fused)

# calibrate the prepared model to determine quantization parameters for activations
# in a real world setting, the calibration would be done with a representative dataset
input_fp32 = torch.randn(4, 1, 4, 4)
model_fp32_prepared(input_fp32)

# Convert the observed model to a quantized model. This does several things:
# quantizes the weights, computes and stores the scale and bias value to be
# used with each activation tensor, and replaces key operators with quantized
# implementations.
model_int8 = torch.quantization.convert(model_fp32_prepared)

# hooks to retrieve inputs, outputs and weights of conv layer (fused conv + relu)
conv_inputs = []
conv_weights = []
conv_outputs = []
hooks = []
for hook in hooks:
    hook.remove()
def hook_fn(m, i, o):
    global conv_inputs, conv_outputs, conv_weights
    conv_inputs = i[0] # [0] because conv_inputs is a tuple and we only care about the first item
    conv_weights = m.weight()
    conv_outputs = o
hooks.append(model_int8.conv.register_forward_hook(hook_fn))

# run forward pass
res = model_int8(input_fp32)

relu = torch.nn.ReLU()

# Manually dequantize and manually compute output 
# Note that convolution is just a simple multiplication because it's a 1x1 kernel with 1 channel
conv_float_input = (conv_inputs.int_repr().int() - conv_inputs.q_zero_point())*conv_inputs.q_scale()
conv_float_weight = conv_weights.int_repr() * conv_weights.q_per_channel_scales()
conv_float_output = conv_float_input * conv_float_weight + model_int8.conv.bias()
manual_output_1 = (relu(conv_float_output / model_int8.conv.scale)).round()
print("manual_output_1:\n", manual_output_1)

# Use built-in dequantize() and manually compute output
# Note that convolution is just a simple multiplication because it's a 1x1 kernel with 1 channel
conv_float_output = conv_inputs.dequantize()*conv_weights.dequantize() + model_int8.conv.bias()
manual_output_2 = relu((conv_float_output / model_int8.conv.scale).round())
print("manual_output_2:\n", manual_output_2)

# Output produced by forward() pass
print("output produced by forward():\n", conv_outputs.int_repr())

# print the difference between manual input and output generated by forward (0.0 means no difference)
print("manual_output_1 and conv_outputs differ by: ", end = "")
print((manual_output_1 - conv_outputs.int_repr()).sum().item())

print("manual_output_2 and conv_outputs differ by: ", end = "")
print((manual_output_2 - conv_outputs.int_repr()).sum().item())

Here’s the output (will differ every time because input is randomly generated):

manual_output_1:
 tensor([[[[ 96.,   0.,  15.,  15.],
          [104.,   0.,   0.,  64.],
          [  0.,   0.,   0.,  31.],
          [  0.,   0.,   0.,   0.]]],


        [[[  0.,  58.,   0.,   0.],
          [ 54.,   0.,  35.,  23.],
          [  0.,   0.,   0.,  17.],
          [ 23.,   8., 125.,  83.]]],


        [[[  0., 125.,   0.,  77.],
          [  0.,  69., 127.,   4.],
          [  8.,   0.,   0.,   0.],
          [ 58.,   0.,  35.,   0.]]],


        [[[ 46.,  15.,  52.,   0.],
          [  4.,  27.,  69.,  29.],
          [  0.,  56.,   0.,   2.],
          [  0.,  54.,  33.,  21.]]]], dtype=torch.float64,
       grad_fn=<RoundBackward0>)
manual_output_2:
 tensor([[[[ 96.,   0.,  15.,  15.],
          [104.,   0.,   0.,  64.],
          [  0.,   0.,   0.,  31.],
          [  0.,   0.,   0.,   0.]]],


        [[[  0.,  58.,   0.,   0.],
          [ 54.,   0.,  35.,  23.],
          [  0.,   0.,   0.,  17.],
          [ 23.,   8., 125.,  83.]]],


        [[[  0., 125.,   0.,  77.],
          [  0.,  69., 127.,   4.],
          [  8.,   0.,   0.,   0.],
          [ 58.,   0.,  35.,   0.]]],


        [[[ 46.,  15.,  52.,   0.],
          [  4.,  27.,  69.,  29.],
          [  0.,  56.,   0.,   2.],
          [  0.,  54.,  33.,  21.]]]], grad_fn=<ReluBackward0>)
output produced by forward():
 tensor([[[[ 96,   0,  15,  15],
          [104,   0,   0,  64],
          [  0,   0,   0,  31],
          [  0,   0,   0,   0]]],


        [[[  0,  58,   0,   0],
          [ 54,   0,  35,  23],
          [  0,   0,   0,  17],
          [ 23,   8, 125,  83]]],


        [[[  0, 125,   0,  77],
          [  0,  69, 127,   4],
          [  8,   0,   0,   0],
          [ 58,   0,  35,   0]]],


        [[[ 46,  15,  52,   0],
          [  4,  27,  69,  29],
          [  0,  56,   0,   2],
          [  0,  54,  33,  21]]]], dtype=torch.uint8)
manual_output_1 and conv_outputs differ by: 0.0
manual_output_2 and conv_outputs differ by: 0.0

[Y_Simson]

I have the same issue. In the forward pass the quantized version is using floating point values for inference.

Any conclusions regarding this?