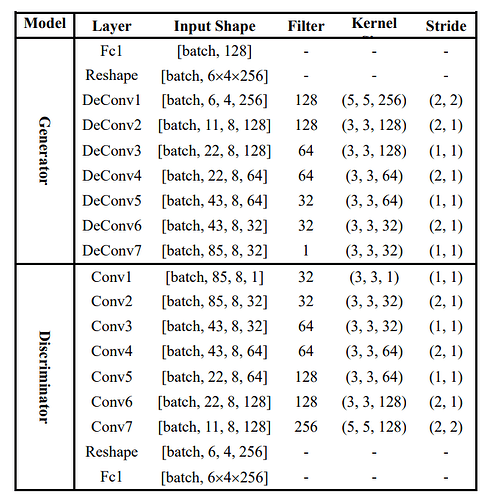
I’m looking to re-implement in Pytorch the following WGAN-GP model:
taken by this paper.
The original implementation was in tensorflow. Apart from minor issues which require me to modify subtle details, since torch seems not supporting padding='same' for strided convolutions, my implementation is the following:
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
self.disc = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=32, kernel_size = 3, stride = (1, 1),padding='same'),
self._block(in_channels=32, out_channels=32, kernel_size=3, stride=(2,1), padding=(1,1)),
self._block(in_channels=32, out_channels=64, kernel_size = 3, stride = (1, 1),padding='same'),
self._block(in_channels=64, out_channels=64, kernel_size = 3, stride = (2, 1),padding=(1,1)),
self._block(in_channels=64, out_channels=128, kernel_size = 3, stride = (1, 1),padding='same'),
self._block(in_channels=128, out_channels=128, kernel_size = 3, stride = (2, 1),padding=(1,1)),
self._block(in_channels=128, out_channels=256, kernel_size=5, stride=(2,2),padding=(2,2))
)
self.lin = nn.Linear(256*6*4,1)
#unifies Conv2d leakyrelu and batchnorm
def _block(self, in_channels,
out_channels,
kernel_size, stride, padding):
return nn.Sequential(nn.Conv2d(in_channels,
out_channels,
kernel_size,
stride,
padding,
bias=False),
nn.BatchNorm2d(out_channels),
nn.LeakyReLU(0.2)) #bias false as we use batchnorm
def forward(self, x):
x = self.disc(x)
x = x.view(-1,256*6*4)
return self.lin(x)
class Generator(nn.Module):
def __init__(self, z_dim):
super(Generator, self).__init__()
self.z_dim = z_dim
self.lin1 = nn.Linear(z_dim, 6*4*256)
self.gen = nn.Sequential(
self._block(in_channels=256, out_channels=128, kernel_size=(5,4),stride=(2,2),padding=(2,1)),
self._block(in_channels=128, out_channels=128, kernel_size=(4,3), stride=(2,1),padding=(1,1)),
self._block(in_channels=128, out_channels=64, kernel_size=(3,3), stride=(1,1), padding=(1,1)),
self._block(in_channels=64, out_channels=64, kernel_size=(3,3), stride=(1,1), padding=(1,1)),
self._block(in_channels=64, out_channels=64, kernel_size=(3,2), stride=(2,2), padding=(1,4)),
self._block(in_channels=64, out_channels=32, kernel_size=(3,3), stride=(1,1), padding=(1,1)),
self._block(in_channels=32, out_channels=32, kernel_size=3, stride=(2,1),padding=(1,1)),
self._block(in_channels=32, out_channels=1, kernel_size=3, stride=(1,1),padding=(1,1)),
nn.Sigmoid()
)
def _block(self, in_channels, out_channels,kernel_size, stride,padding):
return nn.Sequential(
nn.ConvTranspose2d(in_channels,
out_channels,
kernel_size,
stride,
padding,
bias=False),
nn.BatchNorm2d(out_channels),
nn.ReLU(), #they use relu in the generator
)
def forward(self, x):
x = x.view(-1, 128)
x = self.lin1(x)
x = x.view(-1,256,6,4)
return self.gen(x)
The inputs (real/fake/) have shape (batch_size, 1, 85, 8) and consist of very sparse one-hot matrices.
Now, with the above models, during the first training batches I have very bad errors for both loss G and loss D
Epoch [0/5] Batch 0/84 Loss D: -34.0230, loss G: 132.8942
Epoch [0/5] Batch 1/84 Loss D: -3080.0264, loss G: 601.3990
Epoch [0/5] Batch 2/84 Loss D: -216907.8125, loss G: 872.5948
Epoch [0/5] Batch 3/84 Loss D: -26314.8633, loss G: 4973.5327
Epoch [0/5] Batch 4/84 Loss D: -1000911.5000, loss G: 6153.7974
Epoch [0/5] Batch 5/84 Loss D: -14484664.0000, loss G: -5013.7808
Epoch [0/5] Batch 6/84 Loss D: -5119665.0000, loss G: -7194.0640
Epoch [0/5] Batch 7/84 Loss D: -25285320.0000, loss G: 20130.0801
Epoch [0/5] Batch 8/84 Loss D: -11411679.0000, loss G: 32655.1016
Epoch [0/5] Batch 9/84 Loss D: -18403266.0000, loss G: 37912.0469
Epoch [0/5] Batch 10/84 Loss D: -6191229.0000, loss G: 33614.3828
Epoch [0/5] Batch 11/84 Loss D: -8119311.0000, loss G: 28472.3496
Epoch [0/5] Batch 12/84 Loss D: -134419216.0000, loss G: 18065.1074
Epoch [0/5] Batch 13/84 Loss D: -123661928.0000, loss G: 71028.8984
Epoch [0/5] Batch 14/84 Loss D: -2723217.0000, loss G: 47931.0195
Epoch [0/5] Batch 15/84 Loss D: -806806.1250, loss G: 41759.3555
Even though these are just the first batches of the first epoch, the losses seem too large to me and I suspect something’s wrong with my implementation. Or can be normal to obtain such numbers for the WGAN losses at first batches?
If the models look OK, should I upload my training loop for further discussion?
EDIT: I’m adding my training loop as it might help to figure out what’s happening here
opt_gen = optim.Adam(gen.parameters(), lr=0.001)
opt_critic = optim.Adam(critic.parameters(), lr = 0.0001)
# fixed_noise = torch.randn(32, Z_DIM, 1,1)
step=0
gen.train()
critic.train()
for epoch in range(N_EPOCHS):
for batch_idx,real in enumerate(loader):
#Maximizing the distance between the two probabilities p_G and p_data
#TRAIN DISCRIMINATOR max (log(D(x))) + 1-log(D(G(z)))
for _ in range(CRITIC_ITERATIONS):
noise = torch.randn(real.shape[0], Z_DIM,1,1)
fake = gen(noise)
critic_real = critic(real).reshape(-1)
critic_fake = critic(fake).reshape(-1)
gp = gradient_penalty(critic, real, fake, device='cpu')
#we want to maximize here but algorithms like RMSProp are made for minimizing.
# so we just use the trick of putting an extra minus sign.
loss_critic = torch.mean(critic_fake) - torch.mean(critic_real) + LAMBDA_GP*gp
critic.zero_grad()
#retain graph cause we'll use fake for update step of generator.
loss_critic.backward(retain_graph=True)
opt_critic.step()
# TRAIN GENERATOR: min -E[critic(gen_fake)]
output = critic(fake).reshape(-1)
loss_gen = -torch.mean(output)
gen.zero_grad()
loss_gen.backward()
opt_gen.step()
# Print losses and print to tensorboard
print(
f"Epoch [{epoch}/{N_EPOCHS}] Batch {batch_idx}/{len(loader)} \
Loss D: {loss_critic:.4f}, loss G: {loss_gen:.4f}"
)
# with torch.no_grad():
# fake = gen(fixed_noise)
# # take out (up to) 32 examples
# img_grid_real = torchvision.utils.make_grid(
# real[:32], normalize=True
# )
# img_grid_fake = torchvision.utils.make_grid(
# fake[:32], normalize=True
# )
# writer_real.add_image("Real", img_grid_real, global_step=step)
# writer_fake.add_image("Fake", img_grid_fake, global_step=step)
step += 1