Problem with maxium likelihood implementation in PyTorch

1

Recently I am learning to use PyTorch to solve a maximum likelihood problem as described below, and I got a problem with the updates of the parameters.

  1. Data Description
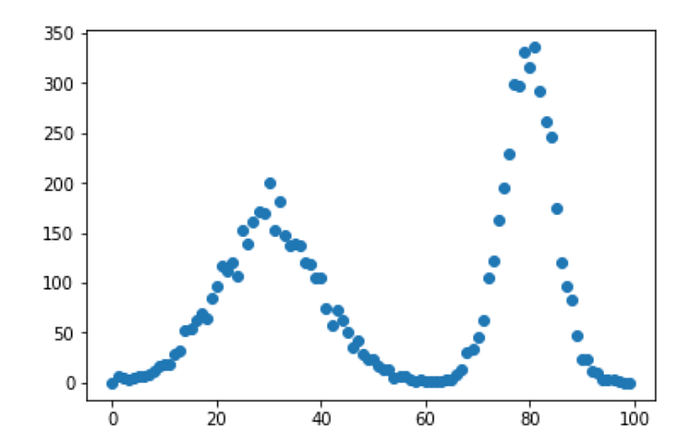
    The data comes from the functionsample_data. It contains 10000 observed value of a random variable, each value denotes the interval it lies.
import numpy as np 

def sample_data():
    count = 10000
    rand = np.random.RandomState(0)
    a = 0.3 + 0.1 * rand.randn(count)
    b = 0.8 + 0.05 * rand.randn(count)
    mask = rand.rand(count) < 0.5
    samples = np.clip(a * mask + b * (1 - mask), 0.0, 1.0)
    return np.digitize(samples, np.linspace(0.0, 1.0, 100))
  1. Problem Description
    for these observed data, I used the maximum likelihood method with the softmax function to fit the distribution of each interval from 0 - 100.
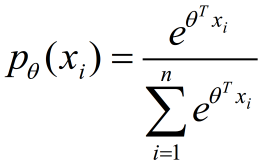
    image75x50

Here x_i is an One-hot encoding vector of the same size with θ, and my reasoning processing for the maximum likelihood is in the below pic.

image
image625×540 27.9 KB

  1. Problem with PyTorch implementation

Here is my implementation for this problem

import torch 
import torch.nn as nn 
from collections import Counter

def sum_x(x):
    dict_item = Counter(x)
    keys_item = dict_item.keys()
    input_of_x = np.zeros((100, 1))
    for key in keys_item:
        input_of_x[key, 0] = dict_item[key]
    return input_of_x

def loss_function(theta, x_fre):
    x = torch.from_numpy(x_fre).float()
    loss = -1/8000 * torch.mm(theta, x) + torch.log(torch.mm(torch.exp(theta), x))
    return loss

X = sample_data()
X_train, X_test = X[:8000], X[8000:]
x_fre = sum_x(X_train)
loss_list = []
theta = torch.zeros((1, 100), requires_grad = True).float()
optimizer = torch.optim.Adam([theta], lr=0.001)

for index in range(1000):
    loss = loss_function(theta, x_fre)
    loss.backward()    
    optimizer.step()
    optimizer.zero_grad()
    loss_list.append(loss)



    
plt.plot(range(len(loss_list)), loss_list)
plt.show()

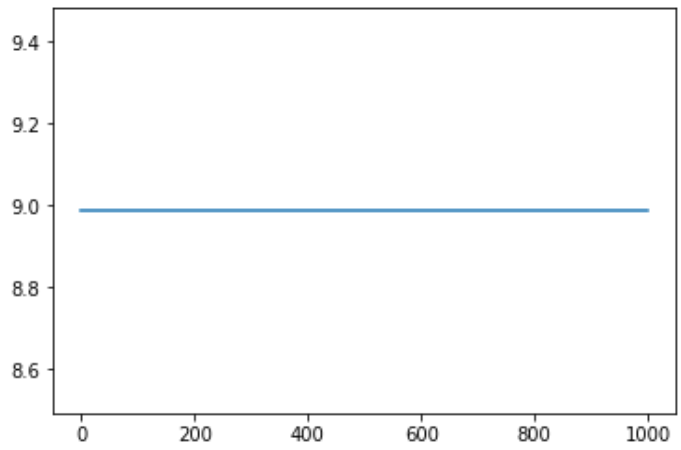
and the result is show as below
image

but the prob distribution should have the shape like mixed of two gaussian for

image
image756×467 43.8 KB
,

It makes me confusing for days. Is anywhere I made a mistake?

Thanks for anyone who can help me with this.

2

Hi Anthony, do you solve this problem? I have similar problen and as I think that weights didnt updated

3

I think that, unfortunately, the program as described has both mathematical and PyTorch errors to make it quite a riddle what is meant.

  • The derivation of the second term of the loss function is not broken. As a result, I would expect to see logsumexp(theta + x, -1) for some appropriately shaped matrix in the loss function.
  • You would want to clamp the reference probabilities away from 0 to avoid -inf negative log likelihood.
  • theta = torch.zeros((1, 100), requires_grad = True).float() makes theta a non-leaf, which is broken. You really, absolutely need to avoid calling any function between constructor and assignment, so here (if it were not the default) one could use use dtype=torch.float in the constructor.
  • There are several other oddities / don't dos. e.g. you should only collect loss.item(), the order of optimizer steps is OK, but the usual way is zero_grad, backward, step etc.

In summary, I would recommend to re-do the derivation unless Anthony has an update that makes the intention and code clearer.

Best regards

Thomas