Pytorch Argrelmax (or C++) function

1

Hello

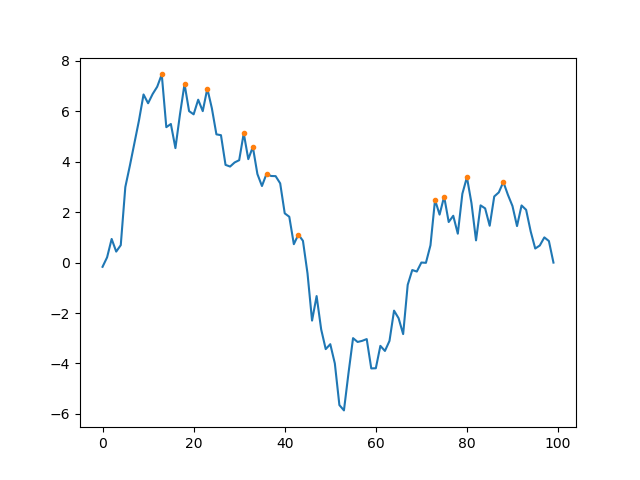
I’m trying to find the equivalent pytorch (or C++) for scipy.signal.argrelmax(), which finds the peaks in a 1D array with some padding. https://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.signal.argrelmax.html

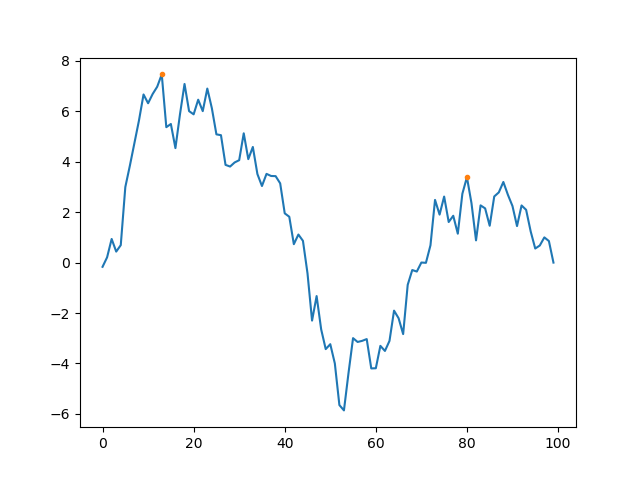
Here’s what I’ve come up with and it is faster than scipy.signal.argrelmax (especially for longer arrays) - but I’m missing a fast solution to the last step which deletes peaks within some window.

import torch

# initalize an array array 
gpu_max = torch.rand(100000)

# find peaks and troughs by subtracting shifted versions
gpu_temp1 = gpu_max[1:-1]-gpu_max[:-2]
gpu_temp2 = gpu_max[1:-1]-gpu_max[2:]

# and checking where both shifts are positive;
out1 = torch.where(gpu_temp1>0, gpu_temp1*0+1, gpu_temp1*0)
out2 = torch.where(gpu_temp2>0, out1, gpu_temp2*0)

# argrelmax containing all peaks
argrelmax_gpu = torch.nonzero(out2, out=None)+1

I posted this on stackoverflow and there’s a picture there that visualize the issue: https://stackoverflow.com/questions/54498775/pytorch-argrelmax-function-or-c.

Any input much appreciated!

2

I’m not sure I understand the precise definition of argrelmax, but you can use maxpooling to determine the absolute maxima of sliding windows. From those (which may reasonably fall on the window boundaries) you could either filter the local maxima, i.e.

N = 200
width = 31 # odd
a = torch.randn(100).cumsum(0)
a -= torch.linspace(0, a[-1].item(), a.size(0))
peak_mask = torch.cat([torch.zeros(1, dtype=torch.uint8), (a[:-2]<a[1:-1]) & (a[2:]<a[1:-1]), torch.zeros(1, dtype=torch.uint8)], dim=0)
b = torch.nn.functional.max_pool1d_with_indices(a.view(1,1,-1), width, 1, padding=width//2)[1].unique()
b = b[peak_mask[b].nonzero()]

pyplot.plot(a.numpy())
pyplot.plot(b.numpy(), a[b].numpy(),'.')

Figure_1

or you could filter which of the window maxima are maxima for the windows around themselves

window_maxima = torch.nn.functional.max_pool1d_with_indices(a.view(1,1,-1), width, 1, padding=width//2)[1].squeeze()
candidates = window_maxima.unique()
nice_peaks = candidates[(window_maxima[candidates]==candidates).nonzero()]
pyplot.plot(a.numpy())
pyplot.plot(nice_peaks.numpy(), a[nice_peaks].numpy(),'.')

Figure_1-1

At least for the example here, the latter coincides with argrelmax output.

Best regards

Thomas

P.S.: I must admit that I usually just skip cross-posted questions because I don’t want to waste my time or that of the people on other forums. Unless questions are a scarcer resource than answers, it is not terribly efficient to have different groups of people look at the same question.

2 Likes
3

Hi Thomas. Thanks so much, the second option seems to match scipy.signal.argrelmax() perfectly. It’s not superfast, but definitely faster than scipy and scales better with increased data length. I’ll also link the stackoverflow answer here - nobody there seemed to know how to do this. Cheers, Cat

4

Can i request for a simular function but for inverted peaks / valleys?

5

You apply the same on -input?

6

Of course

Also, could I request a function that works on a batch if 1D signals…

I wrote something but couldnt paralleize the last part

    peak_mask = torch.cat([torch.zeros((a.shape[0],1), dtype=torch.uint8).bool(), (a[:, :-2]<a[:, 1:-1]) & (a[:, 2:]<a[:, 1:-1]), torch.zeros((a.shape[0],1), dtype=torch.uint8).bool()], dim=1)
    #peak_mask = peak_mask & (a[:] > 0.1)
    b = torch.nn.functional.max_pool1d_with_indices(a.unsqueeze(1), width, 1, padding=width//2)[1].squeeze(1)

    sets = []
    for i in range(0, a.shape[0]):
        bi = b[i,:].unique()
        bi = bi[peak_mask[i,bi].nonzero()]
        #sets.append(bi.flatten().tolist())
        sets.append(bi)
7

Well, assuming you don’t have flats in your peaks, you can easily get them with simple derivates.

Let’s say your input is y, first we get the discrete differences:

dy = tt.diff(y)

Now, a peak is an inflextion point, hence, dy/dx-1
and dy/dx+1 will have different signs, so, we calculate the product of both forward and backward derivates:

sign = dy[:-1]*dy[1:]

(Note that i filtered the first and last elements cause they don’t have dy/dx-1 and dy/dx+1 respectively.)

Then, to get the peaks, just do:

print(sign<0)

If you wanna filter the upper / lower peaks, just add a tt.where() to zero all the non peaks and multiply sign by dy[:-1] or dy[1:] respectively and redo the condition.