I’m not sure I understand the precise definition of argrelmax, but you can use maxpooling to determine the absolute maxima of sliding windows. From those (which may reasonably fall on the window boundaries) you could either filter the local maxima, i.e.
N = 200
width = 31 # odd
a = torch.randn(100).cumsum(0)
a -= torch.linspace(0, a[-1].item(), a.size(0))
peak_mask = torch.cat([torch.zeros(1, dtype=torch.uint8), (a[:-2]<a[1:-1]) & (a[2:]<a[1:-1]), torch.zeros(1, dtype=torch.uint8)], dim=0)
b = torch.nn.functional.max_pool1d_with_indices(a.view(1,1,-1), width, 1, padding=width//2)[1].unique()
b = b[peak_mask[b].nonzero()]
pyplot.plot(a.numpy())
pyplot.plot(b.numpy(), a[b].numpy(),'.')
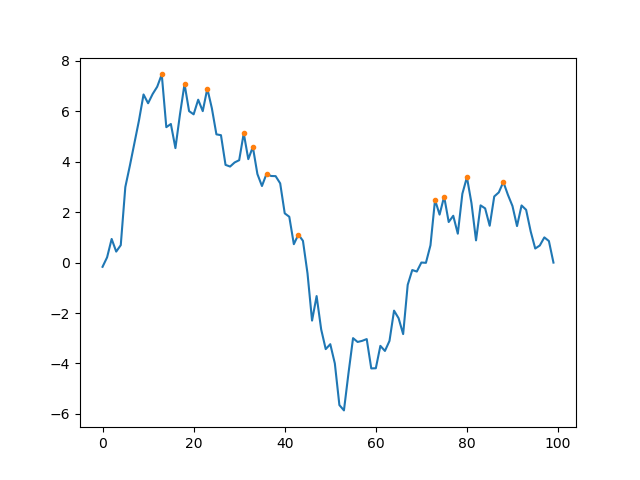
or you could filter which of the window maxima are maxima for the windows around themselves
window_maxima = torch.nn.functional.max_pool1d_with_indices(a.view(1,1,-1), width, 1, padding=width//2)[1].squeeze()
candidates = window_maxima.unique()
nice_peaks = candidates[(window_maxima[candidates]==candidates).nonzero()]
pyplot.plot(a.numpy())
pyplot.plot(nice_peaks.numpy(), a[nice_peaks].numpy(),'.')
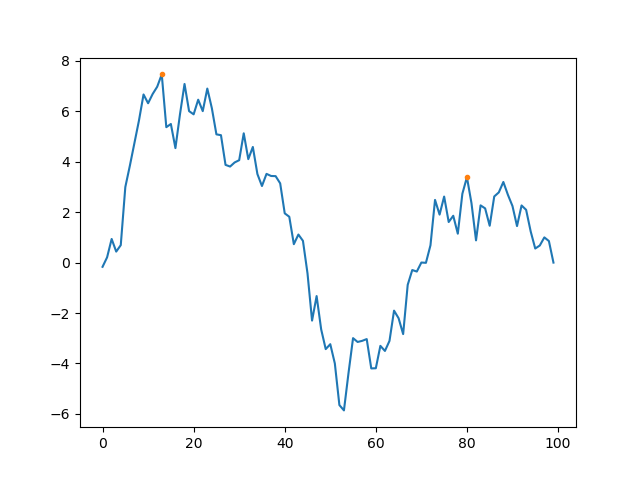
At least for the example here, the latter coincides with argrelmax output.
Best regards
Thomas
P.S.: I must admit that I usually just skip cross-posted questions because I don’t want to waste my time or that of the people on other forums. Unless questions are a scarcer resource than answers, it is not terribly efficient to have different groups of people look at the same question.