PyTorch graphs explanation

1

Hi, I would like to ask some questions about how graphs are computed.

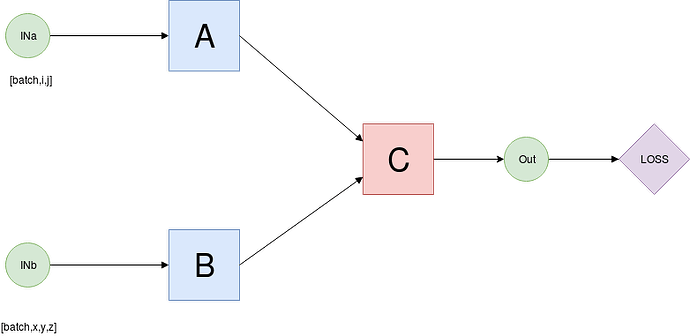
Untitled%20Diagram
Untitled%20Diagram782×381 12.4 KB

Imagine a simple multimodal model where we have 3 sub-networks, A,B,C.

INa and INb are torch variables, with whatever dimensionality but the dimension corresponding to the batch is dim 0, and both have the same amount of samples.

If the proper workflow for one sample were:
A process a sample of INa and B process a sample of INb, then C takes as input OUTa and OUTb to compute OUT.
and so on through the whole batch. When the batch is already processed compute loss and backprop

Is the previously mentioned graph equal to a graph generated by the following process?:
A process the whole batch INa, B process the whole batch INb, then C process the the whole batch OUTa, OUTb and loss-backward?

in pseudo-code:

for i in range(batch_size):
     outa_i = model_A(INa_i)
     outb_i = model_B(INb_i)
     out_i = model_C(outa_i,outb_i)s
stack(out)
loss
backward

for i in range(batch_size):
     outa_i = model_A(INa_i)
outa=stack(outa_i)
for i in range(batch_size):
     outb_i = model_B(INb_i)
outb=stack(outb_i)
for i in range(batch_size):
     out_i = model_C(outa,outb)
out=stack(out_i)

loss
backward

Is there a good explanation about pytorch graphs?

2

They are equivalent graphs.
However, in PyTorch, if you use torch.nn layers, they only know how to do batch processing.

So, your for loop over batch size is redundant, and infact incorrect, because model_A probably doesn’t know how to handle INa_i to give outa_i, but directly does: outa = model_A(ina).
You can fake batch processing by making Ina_i have a batch dimension of size 1.

3

Sorry for the late reply.

I agree with you in case of using by-default torch.nn layers like 2d convolution, which expects to have an extra dimension for the batch. I was wondering what about custom nn.modules

Toy example here

import torch.nn as nn
import torch
import numpy as np

class trial(nn.Module):
    def __init__(self):
        super(trial, self).__init__()
        self.conv = nn.Conv2d(1, 4,kernel_size=3)
    def forward(self,input):
        dims = input.size()
        x = []
        for i in range(dims[0]):
            x.append(self.conv(input[i,:,:,:,:]))

        return dims, torch.stack(x)
class trial2(nn.Module):
    def __init__(self):
        super(trial2, self).__init__()
        self.conv = nn.Conv2d(1, 4,kernel_size=3)
    def forward(self,input):
        dims = input.size()
        x = self.conv(input)
        return x
x = torch.rand(10,1,50,50)
print 'X size {0}'.format(x.size())
m = trial()

y = m(x)
print 'Y size {0}'.format(y[0])

Imagine I have data of 4 dimensions + 1 for batch = 5D
So lets imagine i have groups of 10 images to be processed:
Batch x group x channels x H x W
[5,2,3,50,50]

In this case I have some questions:
is using a for loop over dim 0 the only way to process this batch ?

is the computational graph the same doing m(input) for an input of size [5,2,3,50,50] than doing conv2d(input) for an input size [2x5,3,50,50]? (This is, reshaping all the samples in one dimension)

I’ve seen that in case 2) the graph is

image
image1141×703 35.4 KB

Meanwhile in case of using for loop and more dimensions the graph is
image
image1473×498 39.5 KB

Well obviously it is not, what is the proper way of dealing with data of custom dimensionality not to get improper graphs? Are there some rules about how to proceed at the time of working with multimodal NN?

4

Hi, did you solve this question? I have the same doubt.

5

Hi,
Gradients exist at element level. If you want to run a network several times without duplicating the graph you just need to forward once stacking everything in the batch dimension.