Hello there!
I am new to ML and PyTorch and looking forward to a plenty of interesting discussions in this forum with you guys.
I got stuck into a regression problem for a while. I want my network to learn the relation s(V) between the input vectors V and the target scalar s. s(V) is a very elaborate function of V without constant summands,
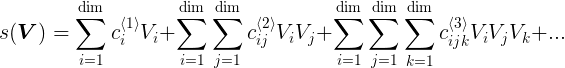
I am given several training and test sets. Until now, I worked with the easiest training and test set. Here the entries of V are small enough to consider s(V) to be linear in V and this simple feed-forward network did the job (with dim=64):
class MyNetwork(nn.Module):
def __init__(self):
super(MyNetwork, self).__init__()
self.lin1 = nn.Linear(dim, 128, bias=False)
self.lin2 = nn.Linear(128, 32, bias=False)
self.lin3 = nn.Linear(32, 1, bias=False)
def forward(self, x):
return self.lin3(F.relu(self.lin2(F.relu(self.lin1(x)))))
There are two major problems that I cannot solve on my own:
Problem 1:
I could achieve an error (standard deviation of the distribution of relative errors over all batches of the test set) of less than 4% within two to three epochs, which is nice, but only when having shuffle in the DataLoader disabled (the training set is uniform and ordered with respect to s). If I set shuffle=True, the smallest errors I get are around 16%, which is miserable. By altering the batch size, learning rate and weight decay I could not solve this problem. Of course, there could be some better combinations of these quantities that I oversee in my manual random search. Unfortunately I have absolutely no clue why that happens.
Question 1 (very general):
In ML, are there scenarios, in which training from a training set that is ordered with respect to the targets is natural? From my understanding so far, one should always try to enable shuffle, such that the most recent backpropagations do not make the network favour any small training subset. But otherwise, if I no longer have to deal with that I could directly skip to
Problem 2:
However, for the next, more difficult training and test set I cannot achieve satisfactory results at all, even if I disable shuffle and optimize the hyperparameters (manually). I figured out this is due to s(V) being no longer approximable as a linear function in V. I vainly tried to add a quadratic part by also processing the outer product of V with itself,
torch.tensor([i*j for j in V for i in V])
into the forward function of my network,
class MyNetwork(nn.Module):
def __init__(self):
super(MyNetwork, self).__init__()
self.lin11 = nn.Linear(64, 128, bias=False)
self.lin21 = nn.Linear(128, 32, bias=False)
self.lin31 = nn.Linear(32, 1, bias=False)
self.lin12 = nn.Linear(64**2, 128, bias=False)
self.lin22 = nn.Linear(128, 32, bias=False)
self.lin32 = nn.Linear(32, 1, bias=False)
def forward(self, x):
return self.lin31(F.relu(self.lin21(F.relu(self.lin11(x))))) + self.lin32(F.relu(self.lin22(F.relu(self.lin12(torch.tensor([i*j for j in x for i in x]))))))
As soon as the training function is called, the following warning is printed out:
[…] line 47, in forward
return self.lin31(F.relu(self.lin21(F.relu(self.lin11(x))))) + self.lin32(F.relu(self.lin22(F.relu(self.lin12(torch.tensor([i*j for j in x for i in x]))))))
ValueError: only one element tensors can be converted to Python scalars
I tried substituting the + by torch.add, but it did not help at all. To be honest, I do not understand this error message.
Question 2:
How can I (elegantly and correctly) introduce higher powers of the input to my neural network (in a similar way to a taylor expansion of second or third order like in the above formula)? Or is there even a non-perturbative way (of course other than guessing the right activation function)?
I am curious about your answers! Thank you very much in advance!