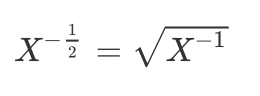Raising a tensor to a fractional power

1

Hi, I need to raise a matrix to the power of -1/2, but I believe doing so using just **(-1/2) makes the computation element-wise.

For example, if I do

m = torch.tensor([[.5,.5],[.7,.9]])
print(m**(-1/2))

I get

tensor([[1.4142, 1.4142],
        [1.1952, 1.0541]])

But what I want is

tensor([[2.6978, -1.1091],
   [-1.5527,1.8105]])

which is what Matlab provides when I run m^(-1/2). Unfortunately torch.matrix_power() seems to only take integers, and torch.pow() also seems to do the computation element-wise.

Thanks!

2

Although it is not best solution, but it will work.
scipy will work without changing torch tensor to numpy as eg.

import scipy.linalg
m = torch.tensor([[.5,.5],[.7,.9]])
print(scipy.linalg.fractional_matrix_power(m, (-1/2)))

array([[ 2.69776664, -1.10907208],
       [-1.55270001,  1.81051025]])
3

Hi mmutic!

A standard approach to exponentiating a matrix is to calculate its
eigendecomposition and then exponentiate the eigenvalues.

Here is a pytorch version 0.3.0 script that illustrates this:

import torch
print (torch.__version__)

m = torch.FloatTensor([[.5,.5],[.7,.9]])           # original matrix

# desired result
mres = torch.FloatTensor ([[ 2.69776664, -1.10907208], [-1.55270001,  1.81051025]])

evals, evecs = torch.eig (m, eigenvectors = True)  # get eigendecomposition
evals = evals[:, 0]                                # get real part of (real) eigenvalues

# rebuild original matrix
mchk = torch.matmul (evecs, torch.matmul (torch.diag (evals), torch.inverse (evecs)))

mchk - m                                           # check decomposition

evpow = evals**(-1/2)                              # raise eigenvalues to fractional power

# build exponentiated matrix from exponentiated eigenvalues
mpow = torch.matmul (evecs, torch.matmul (torch.diag (evpow), torch.inverse (evecs)))

mpow - mres                                        # check result

Here is the output:

>>> import torch
>>> print (torch.__version__)
0.3.0b0+591e73e
>>>
>>> m = torch.FloatTensor([[.5,.5],[.7,.9]])           # original matrix
>>>
>>> # desired result
... mres = torch.FloatTensor ([[ 2.69776664, -1.10907208], [-1.55270001,  1.81051025]])
>>>
>>> evals, evecs = torch.eig (m, eigenvectors = True)  # get eigendecomposition
>>> evals = evals[:, 0]                                # get real part of (real) eigenvalues
>>>
>>> # rebuild original matrix
... mchk = torch.matmul (evecs, torch.matmul (torch.diag (evals), torch.inverse (evecs)))
>>>
>>> mchk - m                                           # check decomposition

1.00000e-07 *
 -0.5960  0.0000
 -0.5960  1.1921
[torch.FloatTensor of size 2x2]

>>>
>>> evpow = evals**(-1/2)                              # raise eigenvalues to fractional power
>>>
>>> # build exponentiated matrix from exponentiated eigenvalues
... mpow = torch.matmul (evecs, torch.matmul (torch.diag (evpow), torch.inverse (evecs)))
>>>
>>> mpow - mres                                        # check result

1.00000e-07 *
  4.7684  7.1526
 -2.3842 -7.1526
[torch.FloatTensor of size 2x2]

You can see that this scheme recovers your Matlab result (actually
Mr. mathematics’s scipy result, because he printed it out with greater
precision).

This will work mathematically for positive semi-definite (square)
matrices (although numerically you will probably want your smallest
eigenvalue to be enough larger than zero that its computation doesn’t
yield a negative value due to numerical error).

However, if you want to use autograd to calculate gradients (for, e.g.,
backpropagation), performing the calculation in scipy won’t work
(unless you write your own .backward() function).

Because the torch.eig() approach works entirely with pytorch tensor
functions, you get autograd / gradients “for free.”

Good luck.

K. Frank

3 Likes
4

This is an old one, so sorry, if my question might be naive, but isn’t this valid for matrix calculation as well?

image

So, if I run this, I get the same result as with scipy:

X.inverse().sqrt()

I assume, this also maintains the gradients?

5

Hi Alfred!

This is incorrect. torch.sqrt() computes the square-roots of the
individual elements of the tensor (not the matrix square-root).

(torch.inverse(), however, does compute the matrix inverse,
rather than the reciprocals of the individual elements.)

Best.

K. Frank

6

Oh sorry, I see. Thanks for the hint :slight_smile: