Hi, I am trying to implement a relative type embedding for transformer based dialogue models, similarily to relative position embedding in https://arxiv.org/pdf/1803.02155.pdf
According to the article the the usual way of computing self attention:
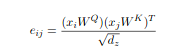
e = torch.matmul(query, key.T)
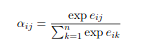
a = torch.nn.functional.softmax(e, dim=-1)
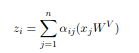
z = torch.matmul(a, value)
is modified to incorporate (by addition) a [batch_size, seq_len, seq_len, embed_dim] sized tensor with the relative position distance embeddings for every position pair in the final z vector. As the position values are the same for the batches, this can be simplified to [seq_len, seq_len, embed_dim] tensor, therefore sparing computation costs.
The modified equation to incorporate the pos embed matrix in self attention is then:
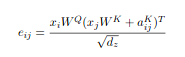
where e can be rewritten as the following to achieve the said optimization of removing the unnecessary broadcasting of the batch dimension:
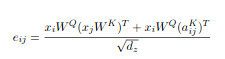
This basically means there are two terms, the first is the regular torch.matmul(query, key.T) product and
torch.matmul(q, pos_embed_mat.T)
The equation for the e tensor in pytorch then can be written as:
e = torch.matmul(query, key.T) + torch.matmul(q, pos_embed_mat.T)
The final output is then:
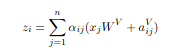
a = torch.nn.functional.softmax(e, dim=-1)
z = torch.matmul(a, value) + torch.matmul(a, pos_embed)
The above code snippets are simplified version of the real code, as these do not take into account the head dimensions and the required various reshape operations to ensure the correct tensor sizes for the matrix products. I use the following function, which produces correct output for correctly shaped input tensors:
def relative_attn_inner(x, y, pos_embed):
"""
x: [batch_size, heads, length, head_dim] or [batch_size, heads, length, length]
y: [batch_size, heads, head_dim, length] or [batch_size, heads, length, head_dim]
pos_embed: [length, length, head_dim] or [length, head_dim, length]
"""
batch_size, heads, length, _ = x.size()
xy = torch.matmul(x, y)
x_t = x.permute(2, 0, 1, 3)
x_t_r = x_t.reshape([length, heads * batch_size, -1])
x_tz = torch.matmul(x_t_r, pos_embed)
x_tz_r = x_tz.reshape([length, batch_size, heads, -1])
x_tz_r_t = x_tz_r.permute([1, 2, 0, 3])
return xy + x_tz_r_t
The whole attention mechanism is then:
def relative_attn(q, k, v, pos_embed):
"""
q: [batch_size, heads, length, head_dim]
k: [batch_size, heads, length, head_dim]
v: [batch_size, heads, length, head_dim]
pos_embed: [length, length, head_dim]
"""
d = value.size(-1) ** 0.5
e = relative_attn_inner(q, k.transpose(2, 3), pos_embed.transpose(1, 2)) / d
a = torch.nn.functional.softmax(e, dim=-1)
z = relative_attn_inner(a, v, pos_embed)
return z
This all works fine, however I am trying to replace the pos_embed tensor with a role_embed tensor, where the elements of the matrix are not the pairwise relative distances of the input tokens, but the 1 or 0 values, whether the given element at position i, j belongs to an utterance spoken by the same person in a context of several turns of dialogs between two agents.
Hi how are you [EOS] Hi I am fine [EOS]
is encoded as
1, 1, 1, 1, 1, 0, 0, 0, 0, 0
1, 1, 1, 1, 1, 0, 0, 0, 0, 0
1, 1, 1, 1, 1, 0, 0, 0, 0, 0
1, 1, 1, 1, 1, 0, 0, 0, 0, 0
1, 1, 1, 1, 1, 0, 0, 0, 0, 0
0, 0, 0, 0, 0, 1, 1, 1, 1, 1
0, 0, 0, 0, 0, 1, 1, 1, 1, 1
0, 0, 0, 0, 0, 1, 1, 1, 1, 1
0, 0, 0, 0, 0, 1, 1, 1, 1, 1
0, 0, 0, 0, 0, 1, 1, 1, 1, 1
This is then fed to a role embedding layer to produce the same [batch_size, length, length, head_dim] sized tensor as the initial pos_embed. However in the case of my role embeddings, the batch dimension can not be simplified, as the embeddings differ for every elment of a batch.
My problem is the above code works for only [length, length, head_dim] sized tensors as this x_tz = torch.matmul(x_t_r, pos_embed) product will have an adittional batch size dimension. Could someone that is interested in this topic help me find a way to rewrite the above equations to fix this problem?
I appreciate any form of help, and also here is a colab link to play with the above code: