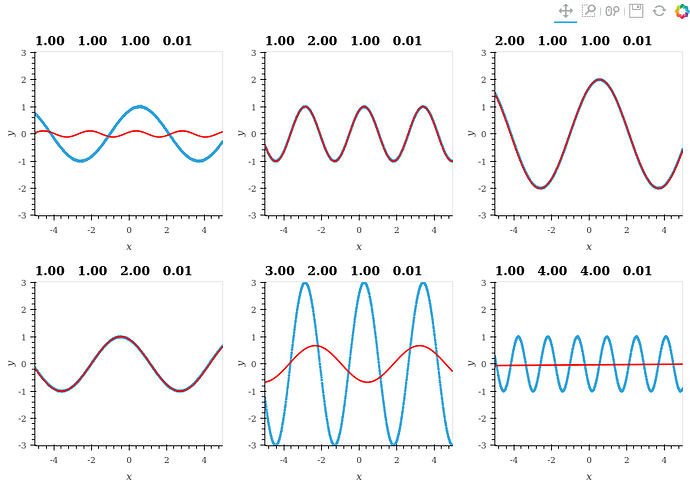
Hi, I’m trying to make a simple fit of the form w1 * sin (w2*x +w3) but the results are somehow strange. Maybe someone can help. Here’s my code:
# create model
import torch
from torch import nn
from torch.autograd import Variable
class MyModel(nn.Module):
def __init__(self):
super(MyModel, self).__init__()
self.w1 = nn.Parameter(torch.Tensor(np.random.randn(1)))
self.w2 = nn.Parameter(torch.Tensor(np.random.randn(1)))
self.w3 = nn.Parameter(torch.Tensor(np.random.randn(1)))
return
def forward(self, input):
w1, w2, w3 = self.w1, self.w2, self.w3
return w1* torch.sin(w2 * input + w3)
import numpy as np
import holoviews as hv
hv.extension('bokeh')
# helper function
def f(w1, w2, w3):
def f2(x):
return w1 * np.sin(w2*x + w3)
return f2
def run_and_plot(w1=1, w2=1, w3=1 ,noise=0.01):
# make some data
x_numpy = np.linspace(-5, 5, 1000)
y_no_noise_numpy = f(w1, w2, w3)(x_numpy)
# add noise
y_numpy = y_no_noise_numpy + noise * np.random.standard_normal(y_no_noise_numpy.size)
# convert
x = torch.autograd.Variable(torch.Tensor(x_numpy),
requires_grad=False)
y = torch.autograd.Variable(torch.Tensor(y_numpy),
requires_grad=False)
# initialize model, optimizer, loss_function
model = MyModel()
optimizer = torch.optim.RMSprop(model.parameters(), lr=0.01)
loss_function = nn.MSELoss()
for epoch in range(1000):
y_pred = model(x)
loss = loss_function(y_pred, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
curf = hv.Points((x_numpy, y_numpy))
curf2 = hv.Curve((x_numpy,y_pred.data.numpy()))
return (curf*curf2).relabel('%.2f %.2f %.2f %.2f' % (w1, w2, w3, noise))
np.random.seed(1)
hv.opts('Curve (color="red")')
(run_and_plot(1, 1 ,1) + run_and_plot(1, 2, 1) + run_and_plot(2, 1, 1)
+ run_and_plot(1, 1, 2) + run_and_plot(3, 2, 1) + run_and_plot(1, 4, 4)).cols(3)
Here’s the resulting plot. Points to fit blue and resulting curve red.
Thanks