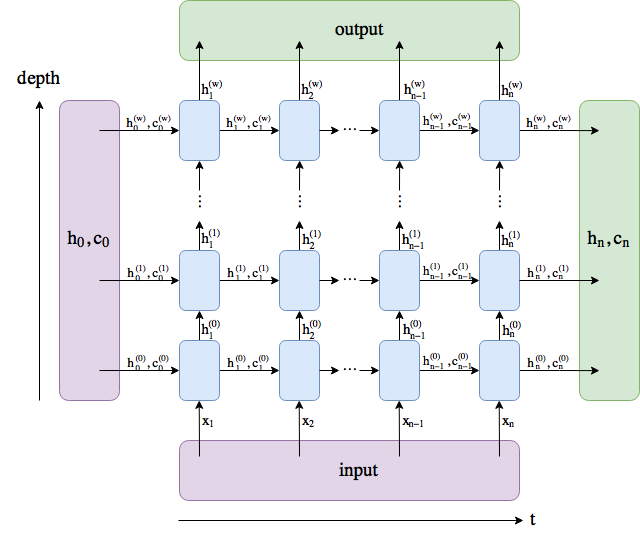
EDIT: I think found my problem. When I do output_last_step = output[-1] I get the last hidden states w.r.t. the forward pass and not the backward pass. The last hidden state w.r.t. the to the backward pass is part of output[0]. self.hidden is independent from seq_len contains only the last hidden states for both passes. I got confused by the figure since it is only for the unidirectional case. If anyone could confirm this, even better.
According to the following figure, I can get h_n^w either from the output of a LSTM (as the output of the last time step n) or the hidden state (for the last layer w):
However, I fail to reproduce it in case of bidirectional LSTMs/GRUs (unidirectional works); below I provide the minimal example. An output will always look like this:
The following 2 tensors should be equal(?)
tensor([ 0.0283, 0.4886, 0.0097, -0.1139, 0.0552, -0.0287])
tensor([ 0.0283, 0.4886, 0.0097, -0.2138, 0.1073, -0.0219])
i.e., the first 3 values representing the forward direction are indeed identical. The values for the backward direction don’t match up. In the unidirectional case, both tensors are the same (obviously with only 3 values).
Moreover, when I do a print(self.hidden[0].data) to check the complete hidden state, the values -0.1139, 0.0552, -0.0287 are nowhere to be found. Using GRU yields the same issue
What am I missing here? Do I misunderstand the return values of LSTM/GRU? Do I make any mistakes in calculating h_n^w using the output or the hidden state?
Here’s the working code:
import torch
import torch.nn as nn
class RnnClassifier(nn.Module):
def __init__(self, bidirectional=True):
super(RnnClassifier, self).__init__()
self.bidirectional = bidirectional
self.embed_dim = 5
self.hidden_dim = 3
self.num_layers = 4
self.word_embeddings = nn.Embedding(100, self.embed_dim)
self.num_directions = 2 if bidirectional == True else 1
self.rnn = nn.LSTM(self.embed_dim, self.hidden_dim, num_layers=self.num_layers, bidirectional=bidirectional)
self.hidden = None
def init_hidden(self, batch_size):
return (torch.zeros(self.num_layers * self.num_directions, batch_size, self.hidden_dim),
torch.zeros(self.num_layers * self.num_directions, batch_size, self.hidden_dim))
def forward(self, inputs):
batch_size, seq_len = inputs.shape
# Push through embedding layer and transpose for RNN layer (batch_first=False)
X = self.word_embeddings(inputs).transpose(0, 1)
# Push through RNN layer
output, self.hidden = self.rnn(X, self.hidden)
# output.shape = (seq_len, batch_size, num_directions*hidden_dim)
# self.hidden[0].shape = (num_layers*num_directions, batch_size, hidden_dim)
# Get h_n^w directly from output of the last time step
output_last_step = output[-1] # (batch_size, num_directions*hidden_dim)
# Get h_n^w from hidden state
hidden = self.hidden[0].view(self.num_layers, self.num_directions, batch_size, self.hidden_dim)
hidden_last_layer = hidden[-1] # (num_directions, batch_size, hidden_dim)
if self.bidirectional:
direction_1, direction_2 = hidden_last_layer[0], hidden_last_layer[1]
direction_full = torch.cat((direction_1, direction_2), 1)
else:
direction_full = hidden_last_layer.squeeze(0)
print("The following 2 tensors should be equal(?)")
print(output_last_step[0].data)
print(direction_full[0].data)
print(self.hidden[0].data)
if __name__ == '__main__':
model = RnnClassifier(bidirectional=True)
inputs = torch.LongTensor([[1, 2, 4, 6, 4, 2, 3]])
model.hidden = model.init_hidden(inputs.shape[0])
model(inputs)