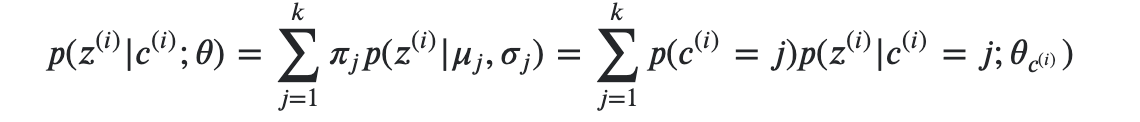Sample from an infinite Gaussian Mixture model

[ZSheikhb (Zahra)]

I have written a code which samples from the infinite Gaussian mixture model, using stick-breaking Dirichlet process. Here z_sample_list is a list of K components coming from the reparameterization trick for each component of z

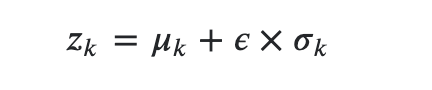
The infinite Gaussian Mixture value is

I think there is a problem in my implementation because the samples don’t look right. I will appreciate if somebody suggests how I can fix this code. I want my code to be able to sample from a distribution similar to MixtureSameFamily but use a similar method as reparameterization trick. Thanks.

def gather_nd(params, indices):
    ndim = indices.shape[-1]
    output_shape = list(indices.shape[:-1]) + list(params.shape[indices.shape[-1]:])
    flatted_indices = indices.view(-1, ndim)
    slices = [flatted_indices[:, i] for i in range(ndim)]
    slices += [Ellipsis]
    return params[slices].view(*output_shape)

def mix_weights( beta):
    beta1m_cumprod = (1 - beta).cumprod(-1)
    return torch.mul(F.pad(beta, (0, 1), value=1) , F.pad(beta1m_cumprod, (1, 0), value=1))


def get_component_samples( batchSize,z_sample_list, z_dim, K, a, b, const_prior,device):
    
    # ensure stick segments sum to 1
    m = Beta(torch.ones_like(a, device=device, requires_grad=False), torch.ones_like(b, device=self.device, requires_grad=False)*const_prior])
    v_means =  m.sample().to(device=device)
    # compose into stick segments using pi = v \prod (1-v)
    pi_samples = mix_weights(v_means)[:,:-1]
    
    # sample a component index   
    
    component = torch.argmax( pi_samples  , 1).to(device=device, dtype=torch.int64)

    component = torch.cat( [torch.arange(0, batchSize, device=device).unsqueeze(1), component.unsqueeze(1)], 1)

    all_z = []
    for d in range(z_dim):
        temp_z = torch.cat( [z_sample_list[k][:, d].unsqueeze(1) for k in range(K)], dim=1)
        all_z.append(gather_nd(temp_z, component).unsqueeze(1))
    
    pi_samples         = pi_samples.unsqueeze(-1)
    pi_samples         = F.pad(input=pi_samples, pad=(0, 0, 1, 0), mode='constant', value=0)
    pi_samples         = pi_samples.expand(-1, K, 1)
    pi_samples         = pi_samples.permute(0,2,1)
    out      = torch.stack( all_z).to(device=device)
    out      = out.permute(1,0,2)
    concatenated_latent_space = torch.bmm(out, pi_samples)

    return torch.squeeze(torch.mean(concatenated_latent_space, 2, True))