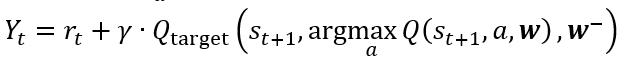SARSA / Q-Learning / Double Q Learning

1

Hello everybody,

I am trying to make SARSA / Q-Learning / Double Q Learning work, but none of them works. Maybe someone can find a mistake in the setup of my problem?

So my world is a simple Markov Model with 2 states and 2 actions.
I modelled x(s,a) as a concatenation of one hot vectors for both, because my states.
I set P[s, a, s’] and R[s, a] so that the ideal policy would be pi(s0) = a0 and pi(s1) = a1. However every algorithm I tried SARSA / Q-Learning / Double Q Learning, it converges to a policy, but not to the optimal one. The interesting thing is that the policy it converges to always has the same action for every state.
I tried every possible value for eps, gamma, learning rate and different periods how often to update the target-weights.

My last hope is, maybe I didn’t understand the formula correctly?
This is my procecudure:

  1. set requires_grad=False on all parameters of Q_target
  2. sample a, observe (s,a,r,s’)
  3. calculate Y and Q= max Q(s,a) and a_max = argmax Q(s,a)
  4. update agent policy (1-eps) → a_max, (eps) → other action
  5. loss = (Y - Q)**2
  6. loss.backward(), optimizer.step(), optimizer.grad_zero()

after couple timesteps copy weights from Q to Q_target

image
image810×518 17.4 KB

2

So I found one error, which is that my network takes concat[s, a] as an argument and outputs a scalar Q. I’ve literally followed the stanford theory lecture, why can’t people indicate the implementation in their damn math formulas?
So this brings me to the question, how do we extract the right Q value in regards to keeping the gradient flow without problems?
Just “Q[a]” , or something like “torch.dot(Q, one_hot(a))”?

Same goes for this part of double DQN:
image
Should we propagate the gradient of the Q network, which is nested inside the Q_target network?