Hi, I’m putting together a basic seq2seq model with attention for time series forecasting. I can’t find any basic guide to achieve this, so I’m following this NLP tutorial. (NLP From Scratch: Translation with a Sequence to Sequence Network and Attention — PyTorch Tutorials 2.2.0+cu121 documentation) and trying to convert it to time series forecasting.
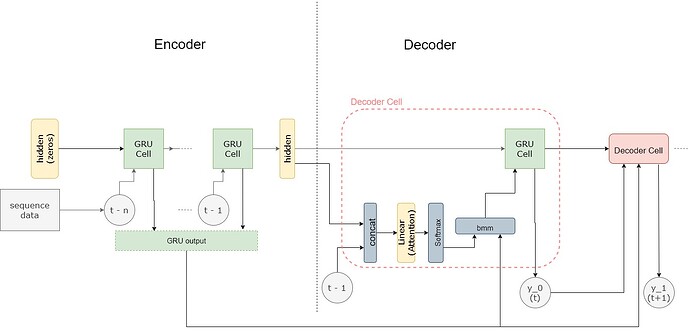
This is the time series model architecture I have now.
I have followed the architecture in the tutorial and removed all the embedding layers needed for NLP.
Following is the code.
class RNNEncoder(nn.Module):
def __init__(self, rnn_num_layers=1, input_feature_len=1, sequence_len=168, hidden_size=100, bidirectional=False):
super().__init__()
self.sequence_len = sequence_len
self.hidden_size = hidden_size
self.input_feature_len = input_feature_len
self.num_layers = rnn_num_layers
self.rnn_directions = 2 if bidirectional else 1
self.gru = nn.GRU(
num_layers = rnn_num_layers,
input_size=input_feature_len,
hidden_size=hidden_size,
batch_first=True,
bidirectional=bidirectional
)
def forward(self, input_seq):
ht = torch.zeros(self.num_layers * self.rnn_directions, input_seq.size(0) , self.hidden_size, device='cuda')
if input_seq.ndim < 3:
input_seq.unsqueeze_(2)
gru_out, hidden = self.gru(input_seq, ht)
if self.rnn_directions > 1:
gru_out = gru_out.view(input_seq.size(0), self.sequence_len, self.rnn_directions, self.hidden_size)
gru_out = torch.sum(gru_out, axis=2)
return gru_out, hidden.squeeze(0)
class AttentionDecoderCell(nn.Module):
def __init__(self, input_feature_len, hidden_size, sequence_len):
super().__init__()
# attention - inputs - (decoder_inputs, prev_hidden)
self.attention_linear = nn.Linear(hidden_size + input_feature_len, sequence_len)
# attention_combine - inputs - (decoder_inputs, attention * encoder_outputs)
self.decoder_rnn_cell = nn.GRUCell(
input_size=hidden_size,
hidden_size=hidden_size,
)
self.out = nn.Linear(hidden_size, 1)
def forward(self, encoder_output, prev_hidden, y):
attention_input = torch.cat((prev_hidden, y), axis=1)
attention_weights = F.softmax(self.attention_linear(attention_input)).unsqueeze(1)
attention_combine = torch.bmm(attention_weights, encoder_output).squeeze(1)
rnn_hidden = self.decoder_rnn_cell(attention_combine, prev_hidden)
output = self.out(rnn_hidden)
return output, rnn_hidden
class EncoderDecoderWrapper():
def __init__(self, encoder, decoder_cell, output_size=3, teacher_forcing=0.3):
super().__init__()
self.encoder = encoder
self.decoder_cell = decoder_cell
self.output_size = output_size
self.teacher_forcing = teacher_forcing
def train(self):
self.encoder.train()
self.decoder_cell.train()
def eval(self):
self.encoder.eval()
self.decoder_cell.eval()
def state_dict(self):
return {
'encoder': self.encoder.state_dict(),
'decoder_cell': self.decoder_cell.state_dict()
}
def load_state_dict(self, state_dict):
self.encoder.load_state_dict(state_dict['encoder'])
self.decoder_cell.load_state_dict(state_dict['decoder_cell'])
def __call__(self, xb, yb=None):
input_seq = xb
encoder_output, encoder_hidden = self.encoder(input_seq)
prev_hidden = encoder_hidden
if torch.cuda.is_available():
outputs = torch.zeros(input_seq.size(0), self.output_size, device='cuda')
else:
outputs = torch.zeros(input_seq.size(0), self.output_size)
y_prev = input_seq[:, -1, :]
for i in range(self.output_size):
if (yb is not None) and (i > 0) and (torch.rand(1) < self.teacher_forcing):
y_prev = yb[:, i].unsqueeze(1)
rnn_output, prev_hidden = self.decoder_cell(encoder_output, prev_hidden, y_prev)
y_prev = rnn_output
outputs[:, i] = rnn_output.squeeze(1)
return outputs
I’m looking to see if there are any black flags in the overall architecture. Does this implementation of global attention make sense for time series forecasting? Currently, I see a slight improvement in my results when compared to a vanilla RNN approach.
Specifically, in the NLP model a START_TOKEN is the first input to decoder, in this case I’m passing the last timestep from X sequence, is this alright?
The attention linear layer is reused in a loop for n future timesteps, does it make sense to maintain a separate layer for each timestep?
And let me know if I can look at any resources to make further improvements to the model.
Thanks ![]()