Sequential LR schedulers

1

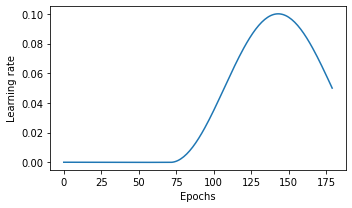
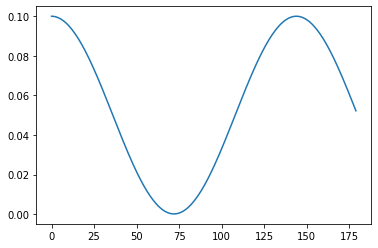
I am not able to build a custom learning rate scheduler using SequentialLR. To elaborate, I am trying to combine CosineAnnealingLR followed by ConstantLR (as per the code below).

I have set the initial learning rate of 0.1

  • I was expecting to have a cosine decay starting from the learning rate of 0.1 and decay to 1e-4 for first 72 epochs
  • Thereafter, for last 18 epochs, I would like to have a fixed learning rate of 1e-4
import torch
import math
from torch.optim.lr_scheduler import SequentialLR, CosineAnnealingLR, ConstantLR
from matplotlib import pyplot as plt

class TinyModel(torch.nn.Module):
    def __init__(self):
        super(TinyModel, self).__init__()
        self.linear2 = torch.nn.Linear(10, 10)
        self.softmax = torch.nn.Softmax()

    def forward(self, x):
        x = self.linear1(x)
        x = self.softmax(x)
        return x

# Set the parameters for learning
num_epochs = 90

model = TinyModel()

optimizer = torch.optim.SGD(
    params=model.parameters(),
    lr=0.1,
    momentum=0.9,
    weight_decay=5e-5,
)

num_steps_optimizer1 = math.ceil(num_epochs * 0.8)
num_steps_optimizer2 = num_epochs - num_steps_optimizer1

scheduler1 = CosineAnnealingLR(optimizer, T_max=num_steps_optimizer1, eta_min=1e-4)
scheduler2 = ConstantLR(optimizer, factor=1e-3, total_iters=num_steps_optimizer2)
scheduler = SequentialLR(optimizer, schedulers=[scheduler1, scheduler2], milestones=[num_steps_optimizer1+1])

lr_schedule = []
for epoch in range(num_epochs):
    # train_epoch(...)
    scheduler.step()
    lr_schedule.extend(scheduler.get_last_lr())

# plotting the simulated LR schedule
plt.figure(figsize=(5, 3))
plt.plot(range(len(lr_schedule)), lr_schedule)
plt.xlabel('Epochs')
plt.ylabel('Learning rate')
plt.tight_layout()
plt.show()

The issue with my implementation is that, the initial learning rate of the CosineAnnealingLR is being determined by the factor that I set for ConstantLR.

More precisely, I observe the following:
with the setting,

scheduler1 = CosineAnnealingLR(optimizer, T_max=num_steps_optimizer1, eta_min=1e-4)
scheduler2 = ConstantLR(optimizer, factor=1e-3, total_iters=num_steps_optimizer2)

I notice the following plot:
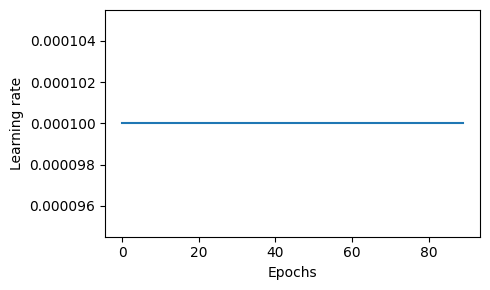
image

and, with the following setting (changed the eta_min in scheduler1),

scheduler1 = CosineAnnealingLR(optimizer, T_max=num_steps_optimizer1, eta_min=1e-5)
scheduler2 = ConstantLR(optimizer, factor=1e-3, total_iters=num_steps_optimizer2)

I notice the following plot:
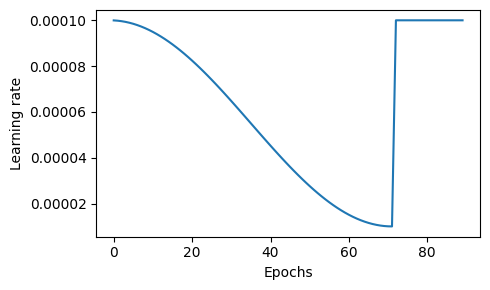
image

So therefore, I conclude that the factor parameter in scheduler2 is influencing the initial learning rate for scheduler1.

I would appreciate any insights and guidance on how to overcome this issue.

2

I don’t believe scheduler2 has any influence in scheduler1 and you would see the same effect by removing it:

scheduler1 = CosineAnnealingLR(optimizer, T_max=num_steps_optimizer1, eta_min=1e-5, verbose=True, last_epoch=-1)

lr_schedule = []
for epoch in range(num_epochs*2):
    optimizer.step()
    scheduler1.step()
    lr_schedule.extend([optimizer.param_groups[0]['lr']])

# plotting the simulated LR schedule
plt.figure(figsize=(5, 3))
plt.plot(range(len(lr_schedule)), lr_schedule)
plt.xlabel('Epochs')
plt.ylabel('Learning rate')
plt.tight_layout()
plt.show()

which shows:
image

To be honest, I don’t fully understand why the learning rate starts at eta_min since it doesn’t seem to fit the posted formula in the docs:

nmax = 0.1
nmin = 1e-4
Tmax = 72

a = []
for Tcur in range(num_epochs*2):
    a.append(nmin + 0.5 * (nmax - nmin) * (1 + np.cos(Tcur/Tmax * np.pi)))
    
plt.plot(a)

image

But maybe I’m using it wrong and @albanD can correct me.

3

I’m afraid I don’t know :confused:
We would need to dive into the code.