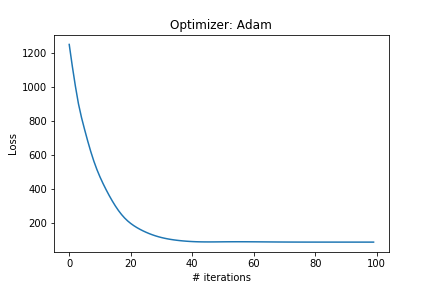
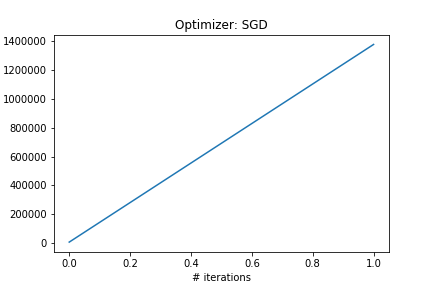
I’m using torch version 1.0.0.
I am trying to perform a gradient descent optimization using two different optimizers: SGD and Adam from the optim package. Strangely, while the loss function obtained by Adam converges and is steadily decreasing, the loss with SGD increases dramatically from the start and contains nan after just a few iterations.
This is true for different learning rates, momenta and also after adding regularisation terms.
Why is this??
Below is the code. You will not be able to run it as is as it imports some of my classes but I will be happy to provide anyone with the rest of the code if need be. The important part is the gradient descent loop at the end:
import torch
import torch.nn as nn
import torch.optim as optim
import HiddenStatesModel as HSM
import numpy as np
import matplotlib.pyplot as plt
def S(x):
return 1/(1+torch.exp(-x))
sft = nn.functional.softmax
def forward(StatesVec, kappa, rho, L, dt):
lbd = 1/8
StatesVec = StatesVec + (kappa*(-lbd*StatesVec -rho.mm(S(StatesVec)) + torch.ones(N,1,dtype=torch.float64)))*dt
# Use factor 2 in sft() to have a "stronger" softmax function
pos = L.mm(sft(StatesVec*2, dim=0))
return StatesVec, pos
timesteps = 1100
N = 6
dt = 0.1
"""Create connectivity matrix rho"""
rho = torch.zeros(N,N,dtype=torch.float64);
for i in range(N):
for j in range(N):
if i == j:
rho[i, j] = 0
elif j == i + 1:
rho[i, j] = 1.5
elif j == i - 1:
rho[i, j] = 0.5
else:
rho[i, j] = 1
rho[-1, 0] = 1.5
rho[0, -1] = 0.5
process = HSM.GenerativeProcess()
Ltrue = np.array([[1,1.1,1,1.2,1.4,1.3],
[1,1.2,0.4,1.3,0.9,0.6]]);
OBStrajectory, HSPtrajectory = process.run(N, 2, timesteps, Ltrue[:, 0:N], dt=dt)
target = torch.tensor(OBStrajectory, requires_grad = False, dtype = torch.float64)
"""L and kappa will be inferred. Randomly initialise L, set initial kappa to 5.5"""
L = torch.tensor(np.random.randn(2,N),dtype = torch.float64, requires_grad = True)
kappa = torch.tensor(5.5, requires_grad = True, dtype = torch.float64)
iterations = 100
losses = []
optimizer = optim.SGD([L, kappa], lr = 0.05, momentum = 0.0)
#optimizer = optim.Adam([L, kappa], lr = 0.05)
for _ in range(iterations):
"""Initialise States Vector"""
StatesVec = torch.tensor(HSPtrajectory[:, 0]).view([6, 1])
"""HS stands for Hidden States"""
HSHistory = np.zeros([6, timesteps])
loss = 0
for t in range(timesteps):
StatesVec, pos = forward(StatesVec, kappa, rho, L, dt)
HSHistory[:, t] = StatesVec.clone().detach().numpy()[:, 0]
loss += torch.sum((pos - target[:, t].view(2,1))**2)
losses.append(loss)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print("Iteration no %d"%_)
plt.figure()
plt.plot(losses)
plt.ylabel('Loss')
plt.xlabel('# iterations')
plt.show()